#QED SYSTEMS

[ace-trainguys]

Whumptober day 25 - prompt is lost voice.

Imagine how much tougher of a time Ingo would have if he lost his voice in addition to his memories. His main way of expressing himself is through speech - without it, he’s an unapproachable silent, stoic man. Very few in the Pearl Clan would be willing to interact with him.

#whumptober2022 #no.25 #lost voice #submas #art #ingo #qed's art #this would be like soon after he lands in Hisui #as soon as he's well enough to walk around #I'd say he probably would be kicked out of the clan asap except Lady Sneasler took a liking to him #I like to hc that Emmet and Ingo know sign language #in this situation no one in Hisui does #He gets called 'stranger' and 'outsider' until he's able to write his name down #bonus points if you want there to be a difference in writing systems #then he has to learn a whole new writing system before he can even be called by name #I had an idea for a cute bonus to this but I have gotten busy recently and I didn't have the time #perhaps something to return to after whumptober

[megarywrites]

Currently working up to this setting/character intro and scene that i’ve been daydreaming about for M O N T H S i’m so excited i hope i do it all justice

#writing journal #wip: seafoam #we’re about to reach the final mother figure character and she should be considered the final boss of mother figures #(i don’t play video games idk what i’m talking about) #but the setting is gorgeous and it’s finally the opportunity to get into the Greacian magic system #(as well as hint at bits of the Qed magic system) #like i said #daydreaming for ages

[theaudiophileman]

#audiophile #hifi #audio #audio system #hifidelity #technology #new #listen #reviews #review #cables #speaker cable #QED #speakers

[qqueenofhades]

as someone whose family immigrated here from the global south, somewhere these online leftists claim to give a shit about, it baffles me that a) a lot of them are white and b) a lot of said white people constantly whine about being powerless in this system while the numbers show that white people above 30 still vote majority republican. something these white leftists could do is spend some time convincing their parents and grandparents to stop voting red and yanking this country backward with the gop, but that's unglamorous and being a bootlicker for the establishment, apparently.

the white guilt just bothers me so much because there are things that they can do, plenty, in fact, but those don't win them outrage points on the internet. i always wonder with them, do they actually want things to get better, or do they prefer them continuing to get worse bc good things don't give ways to generate clout from complaining

I mean yeah, you've kind of nailed it there. They want outrage points on the internet (and while insisting that America is the only country that causes all evil in the world, they also think that everyone else is merely a helpless puppet manipulated by American evil, and not an actual person, country, or entity able to make its own choices). They know what they should be seen to care about, and maybe some of them actually do, but they refuse to engage in any meaningful way that could make that change, because it is Morally Impure (whether voting for Democrats or acknowledging that voting has any power at all and the two parties are not the same by trying to get their parents/grandparents to stop voting Republican). The more morally self-righteous you can look on the internet, the more popular you are on Leftist Twitter, so.... QED.

#anonymous #ask #politics for ts

[lukore]

pact: a story about qed-ing the shit out of your opponent—using a self-contained imperialist system of extremely esoteric rules baked up by a wizard—so hard that all onlookers point and laugh: holy shit that guy got owned! and thus it becomes true; he did get owned

worm: a story about deploying a bunch of diverging epistemologies in a kodoku and looking on in terror and awe at what toxic shit comes out. also god is dead, smth smth death drive?

#parahumans

[saddest-girl-in-the-whole-world]

I appreciate your Pratt!Babs vision, obviously. However, I feel that Chris Pratt wouldn't want to be cast as a character who spends most of his time as a chew toy, and he seems too posh for his vocal delivery - I can't picture him voicing "you cut too much" or "why's the food so bad? QED, it's a conspiracy", he's usually the guy who delivers the punchline with a shit-eating grin. So I raise you an even more cursed option: Chris Pratt as an aged-down Teacher.

You know I'm not even sure if I agree but these images sent me into a giggling fit, also "Pratt!Babs" sent me into two more giggling fits

Maybe he'd just play both how about that, I can incorporate that into my belief system

#asks #what a day #i dont think ive been insulted this much in my life #im having a great time

[solarpoweredbirds]

OK SO here's that separate post i was talking about in the tags of my last rb

i recently learned* you can have completely normal levels of total testosterone but high levels of "free" testosterone (testosterone that your body can use). your body has sex hormone binding globules (sbhg's) which bind to, well, sex hormones, and prevent them from working to regulate the levels of sex hormones more accurately. if those levels are low for whatever reason, it means that more of the testosterone in your body is available for use. while i'm sure that's not the only potential cause, my point is that you VERY MUCH can have "normal" levels of testosterone (if we ever figure out what those are) and have "hyperandrogenism" (loaded term because hirsutism is usually the main symptom and has a...pretty racist history but you get the point).

as a note on that though, low shbg levels can often be associated with congenital adrenal hyperplasia, which can cause health issues beyond just hyperandrogenism. so if you have hyperandroginism caused by that, it's worth looking into other issues you may have possibly being related!

tl;dr there are LOTS of reasons for "hyperandroginism", and yes, sometimes (probably more frequently than the medical system wants to admit) it just Happens due to natural variations! but also, in some cases it can be associated with other issues. so if you have issues that you have yet to find any reasonable explanation for and symptoms of high testosterone, it's worth looking into hormonal imbalances/related conditions because sex hormones DO interact with other hormones and body processes and that's important to keep in mind!

*by "recently learned" i mean i was going through old bloodwork and found out that this was the case for me pre-t because my doctor just said "yeah your testosterone is highish" and didn't elaborate. qed, it can be very beneficial to learn to read your own bloodwork (i know at least for usamericans, quest diagnostics lets you access your bloodwork online and has short descriptions of each test's meaning, but you can easily find more detailed ones online!)

#my post #sorry if this is something no one cares about but i am very passionate about it lol #The Tism. you know? #but i do hope that this manages to reach someone it can help! #hyperandrogenism #cah #ncah #testosterone

[mitigatedchaos]

Considering taking a hardline stance (I think I already believe this TBH, just haven't, like, mathematically rigorously thought it out) that, ignoring other factors unrelated to automation itself, it is always good in net when technology puts people out of work. This is because paid labor is by definition shit that people want done but people don't want to do. QED it's better if it can get done without people doing it.

You kinda have to ignore those other factors, because @playinghardtolistento makes a great criticism:

What I’m worried about is that even the left-rationalists appear to be mainly interested in UBI, a policy whereby those who own the systems that have eliminated the economic position of most of the population provide them a portion of their surplus, as an ultimately revocable privilege in exchange for giving up all actual self-determination.

I would argue that a UBI does provide some level of self-determination, because being able to choose what to buy is a big deal, but that it reduces leverage to have no other options for income is undeniable.

You can think of this as the flip-side of the coin for the UBI Police State hypothesis. In the UBI Police State, the UBI allows the creation of a permanent protest class who can spend all their time obstructing productive infrastructure, who have limited prospects to improve their lot by actually working. For the system to function, someone has to send in the riot cops to physically drag the hippies out of the refineries, or real production will fall and inflation will degrade the value of the UBI.

Playhard here comes at this from the opposite direction - because they're superfluous to the production process, except as a pool of potential reserve labor that suppresses wages, people pushed out of the economy by automation (assuming the automation works that way) have reduced leverage because they can't harm the material interests of the owners of capital merely by going on strike.

This is actually a really tough problem to manage. One reason it's tough is that economic planning is naturally difficult, and the median person can't necessarily be trusted to run a business. "Social ownership of the means of production" risks just meaning "politicians run all the businesses." (A big part of capitalism is also that firms are expendable, so if they become too dysfunctional, they can be replaced.)

One first approximation is to use direct-to-labor wage subsidies combined with a very low minimum wage, to reduce job losses to automation in industries where we would just have to pay out welfare anyway, while keeping people involved in the production process. This is probably less psychologically damaging to people than feeling they're completely unneeded, and it's more robust in the event of program termination since they still have some income from a productive enterprise.

But over the long-term, we're probably going to have to rethink the ownership model.

This is actually quite challenging, as "private property rights" has done fairly well at human freedom and productive enterprise compared to competitors. Alternatives often have pretty significant incentive problems (and may incentivize poverty, including famine).

What we probably want is not a UBI, but a redistribution of land rents and material rents to prevent being unable to earn a living due to being outbid for all the inputs for production.

#anons #asks #politics

[wumblr]

Far away in the heavenly abode of the great god Indra, there is a wonderful net which has been hung by some cunning artificer in such a manner that it stretches out infinitely in all directions. In accordance with the extravagant tastes of deities, the artificer has hung a single glittering jewel in each "eye" of the net, and since the net itself is infinite in dimension, the jewels are infinite in number. There hang the jewels, glittering "like" stars in the first magnitude, a wonderful sight to behold. If we now arbitrarily select one of these jewels for inspection and look closely at it, we will discover that in its polished surface there are reflected all the other jewels in the net, infinite in number. Not only that, but each of the jewels reflected in this one jewel is also reflecting all the other jewels, so that there is an infinite reflecting process occurring.

As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable couplings which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances. In quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the dressed electron seen at large distances, and this change, or running, in the value of the electric charge is determined by the renormalization group equation.

The dependence in MOND of the internal dynamics of a system on its external environment (in principle, the rest of the universe) is strongly reminiscent of Mach's principle, and may hint towards a more fundamental structure underlying Milgrom's law.

Indeed, the potential link between MONDian dynamics and the universe as a whole (that is, cosmology) is augmented by the observation that the value of a0 (determined by fits to internal properties of galaxies) is within an order of magnitude of cH0, where c is the speed of light and H0 is the Hubble constant (a measure of the present-day expansion rate of the universe). It is also close to the acceleration rate of the universe, and hence the cosmological constant. However, as yet no full hypothesis has been constructed which manifests these connections in a natural way.

[perkuneaudio]

Unleash the Power of Sound: Finding the Best Loudspeaker Cables Online

In the sector of audio fanatics, the pursuit of perfect sound best is an ongoing adventure. Whether you are a song aficionado, a home theater fanatic, or a professional sound engineer, the significance of awesome loudspeaker cables can't be overstated. These cables serve as the lifeline between your audio additives, transmitting alerts with precision and readability.

The Role of Loudspeaker Cables

Loudspeaker cables play a vital role inside the transmission of audio indicators from your amplifier or receiver on your audio system. Unlike other cables, consisting of HDMI or USB, which transmit digital records, loudspeaker cables cope with analog alerts. As such, their production and pleasant significantly impact the constancy of sound replica.

Factors to Consider

When shopping for loudspeaker cables online, numerous elements come into play to ensure excellent performance. Firstly, gauge size is paramount. Thicker cables, normally indicated through a decrease in electrical resistance, taking into consideration better conductivity and decreased sign loss over longer distances.

The Importance of Terminations

Terminations, or connectors, are the interface among your loudspeaker cables and your audio additives. Common termination types consist of banana plugs, spade connectors, and bare cord ends. Each type offers its benefits, from comfort to more desirable connectivity.

Top Picks: Best Loudspeaker Cables Online

Now that we've protected the fundamentals, let's discover some top alternatives for loudspeaker cables to be had on line.

1. Perkune Type 4 Speaker Cable

Renowned for their dedication to audio excellence, Perkune gives the Type 4 Speaker Cable as a top rate preference for audiophiles. Featuring strong conductors made of high-purity copper and a unique geometry, this cable grants exceptional readability and backbone. With its flexible layout and to be had termination alternatives, along with banana plugs and spade connectors, the Perkune Type four gives versatility and performance in identical measure.

2. Kimber Kable 8TC Speaker Cable

Crafted with meticulous attention to element, the Kimber Kable 8TC Speaker Cable embodies the pursuit of sonic perfection. Its specific braided layout minimizes electromagnetic interference at the same time as maintaining sign integrity. The use of Kimber's proprietary VariStrand™ generation guarantees uniform conductivity for the duration of the cable, ensuing in a balanced and natural sound reproduction. Whether used in a stereo device or a multi-channel setup, the Kimber Kable 8TC supplies an immersive listening enjoy.

3. QED XT25 Speaker Cable

Combining affordability with uncompromising overall performance, the QED XT25 Speaker Cable is a standout choice for price range-conscious audio fanatics. Engineered with QED's X-Tube™ era, this cable minimizes skin effect and impedance version, keeping the integrity of the audio sign. The low-loss dielectric guarantees minimum sign distortion, taking into account particular sound reproduction throughout the frequency spectrum.

Continuing Your Journey

As you embark for your quest for the perfect loudspeaker cables, recollect delving deeper into the following topics to increase your information: In conclusion, locating the best loudspeaker cables online entails cautious attention of things including gauge length, cloth composition, and termination options. By understanding those key aspects and exploring top choices from legitimate producers, you can increase your audio revel in to new heights.

#Best Loudspeaker Cables Online

[hayingsang]

What I read in 2022

A little late. 2023 to follow soon.

* * *

Ying Shih Yü, Chinese History and Culture, Volume 1

Yuen Yuen Ang, China’s Gilded Age

Lucia Berlin, A Manual for Cleaning Women

Stephan Körner, Kant

Alexander Herzen, My Past and Thoughts, Vol 5

Leonard Susskind & George Hrabovsky, Classical Mechanics: The Theoretical Minimum

Frank Dikotter, Mao’s Great Famine

Alexander Herzen, My Past and Thoughts, Vol 6

George Orwell, 動物農莊（港豬版）

Tom Hopkins, Sales Prospecting for Dummies

Ray Bradbury, Fahrenheit 451

Paul Gilroy, There Ain’t No Black in the Union Jack

Kenn Amdahl, There Are No Electrons

Gianfranco Poggi, The Development of the Modern State

Ehrhard Bahr & Ruth Goldschmidt Kunzer, Georg Lukacs

Gianfranco Poggi, Forms of Power

Thomas Gordon, Parental Effectiveness Training

Robert Heinlein, Starship Troopers

James Fok, Financial Cold War

Angela Carter, The New Eve

Elizabeth Strout, My Name is Lucy Barton

Ying Shih Yü, Chinese History and Culture, Volume 2

Bill Hayton, The Invention of China

Murasaki Shikibu, The Tale of Genji

Hannah Arendt, The Life of the Mind

林匡正, 香港足球史

Karl Ulrich & Lele Sang, Winning in China

Harry Morgan, Sunny Places for Shady People

Elizabeth Strout, Amy and Isabelle

Naomi Standen (ed), Demystifying China

Angela Carter, Wise Children

Elizabeth Strout, The Burgess Boys

John Gribbin, Get a Grip on Physics

Chris Waring, An Equation for Every Occasion

Hannah Arendt, The Human Condition

Mary McCarthy, Birds of America

Mary McCarthy, The Company She Keeps

Lisa Taddeo, Three Women

Hon Lai-chiu, The Kite Family

Jim Breithaupt, Physics

John Gribbin, Seven Pillars of Science

John Gribbin, Six Impossible Things

Barry Lopez, Horizon

Elizabeth Strout, Olive Kittridge

Elizabeth Strout, Anything is Possible

Elizabeth Strout, Oh William!

Mike Goldsmith, Waves

Monica Ali, Untold Story

Catherine Merridale, Ivan’s War

Jessica Andrews, Saltwater

Val Plumwood, Feminism and the Mastery of Nature

AM Homes, May We Be Forgiven

Gaia Vince, Adventures in the Anthropocene

Ho-fung Hung, City on the Edge

Richard Feynman, QED

Fredric Raichlen, Waves

Angela Carter, The Magic Toyshop

Karen Cheung, The Impossible City

Adam Tooze, The Deluge

Celeste Ng, Everything I Never Told You

Sean Carroll, The Biggest Ideas in the Universe

Louisa Lim, The Indelible City

Gavin Pretor-Pinney, The Wave Watcher’s Companion

Adam Tooze, The Wages of Destruction

Adam Tooze, Shutdown

Annie Ernaux, A Frozen Woman

Ursula Le Guin, The Lathe of Heaven

Virgina Woolf, The Waves

Ursula Le Guin, Tehanu

Ursula Le Guin, The Telling

Gaia Vince, Nomad Century

Janna Levin, How the Universe Got Its Spots

Lara Alcock, Mathematics Rebooted

Donella Meadows, Thinking in Systems

Emily St John Mandel, The Glass Hotel

Anon, 伊索傳 & 驢仔

Elizabeth Kolbert, Under a White Sky

Emily St John Mandel, Station Eleven

Gary Gerstle, The Rise and Fall of the Neoliberal Order

Bruno Mansoulié, All Of Physics (Almost) In 15 Equations

[thecurioustale]

Why are you ass kissing the latest mutt in a line of mongrels who raped and barbarized my country for centuries? Does your ‘leftism’ stop when us Asians are mentioned? Do you think what the British crown inflicted on China was deserved? Do you think my ancestors deserved to be enslaved and hooked on opium by that animal’s family?

I hope Charles and the rest of his ilk get exactly what they deserve for what his incest fueled bloodline did to mine and millions if not billions of others.

I don't normally feed the trolls, and future anonymous asks on this subject will be deleted, but this ask is a good QED to what I was saying earlier.

This is blind hatred, generational hatred, ethnic hatred—all from the comfortable immunity of anonymity. Hatred without accountability. No consequences. Not even enough courage to put their username on the ask. Cowardice.

It is ugly.

It is a side of humanity that foments murder and torture. This anon is just jealous that it wasn't them (most likely "him") who got to commit the atrocities. They are projecting their own malice onto Charles. Probably, they are projecting a lifetime's pent-up sense of powerlessness, and their resentment toward the whole world, onto him.

Charles was a kid when the British Empire was dissolving, and the British Crown was long since subordinated to the British parliamentary system of democracy. It wasn't kings who ran the Empire; it was elected representatives of the people, and it certainly wasn't this king. Charles is not your enemy, anon. He has lived a life of public service inside a fishbowl of incessant scrutiny, and few of us would hold up so well to that. He reminds me of countless overprivileged, well-off, safely moderate-liberal yuppies I've met over the years. I can name many public figures far worse, who still don't deserve the punishment you wish for.

And he's rich and he's a king and he doesn't need me to defend him, and I'm not trying to. But I've spent my whole life speaking out against mob insanity, scapegoating, and the perils of malevolence among us. This is not acceptable behavior. I'm sure some of the people who do it are just "blowing off steam." (It's a tidy little excuse, that, for behaving with the attitude of a killer.) And I'm sure others really do mean it and, were it not for fear of the law, would go out a-murdering right now.

To answer the questions put to me: No. No, I don't think that what horrors the British did in China, or anywhere else, were deserved. No, I don't support slavery. No, I don't support addicting people to drugs for profit. What ridiculous questions. What a disingenuous conflation of ideas. And what an utterly artless strawman argument. It fools no one.

I have a hard time coming to terms with this kind of human mind. I struggle to imagine what it is even like to experience. I do know what contempt and resentment feel like, of course. I even know what hate feels like—and from me it is a hard-earned thing. And, yes, there are some people out there who I think deserve the death penalty: human traffickers; many types of sex abusers; the most dangerous fascist exponents. You know...people who are actively committing grievous crimes themselves. None of this "generational guilt" bullshit, which would be like me wanting to murder contemporary German politicians for what their long-ago predecessors did to my ancestors.

But even on the people I hate, and who I think deserve the death penalty, I would not and do not wish torture and suffering. I can't bring myself to feel that way; even in my fantasies I can't do it—nor do I especially try. I do not understand the sheer meanness of it, the fundamental and profound failure of empathy. I have spent a great portion of my life writing about this in contemplation, both in fiction and non-fiction, and I still do not understand it. To use the anon's own language against them, I do not understand the animality of it. It's barbaric. It really makes me question what goes on in some people's brains.

My earlier post wasn't a defense of British royalty. I do have some sympathy for the British monarchy in its present form as a living historical institution of English culture, and I admit to being allured by all the finery and pomp, and by the quiet lifelong dignity of the late Queen Elizabeth—and you can cringe away from me for that fairly if you wish—but I'm not truly invested in British royalty and I don't believe in hereditary forms of government, and I know that, as someone with a Jewish background, I would have been a victim of British policy myself had I lived there or in its empire in bygone times. And I'm certainly not going to waste my self-imposed limited credits for broaching political subjects here on Tumblr just to stan the King of England.

My earlier post was an observation that, just a couple of steps away from this kind of murderous impulse toward the British Crown, there is fierce anti-Semitism, the hatred of Jews, the attempt to delegitimize the Israeli people and all Jews by extension. That's not a coincidence: Blind hatred often expresses itself in many different ways. Hence the "weird tells" I was talking about. And I find it additionally telling that the anon did not mention this part of it at all. People who act in bad faith never actually consider what you say; they just rail against the parts of it they don't like.

That's all I'm going to say about this. I'm sure many of you don't like reading this stuff. I certainly don't. I hope those of you who have bothered to read this take my core message to heart: This kind of malevolence is not acceptable, no matter who or where it comes from. Many, many evils spring from it, and it represents something terrible about human nature.

Beware of it.

#Philosophy of hate

[theresearchblog]

Investment Management Software Market is set for a Potential Growth Worldwide: Excellent Technology Trends with Business Analysis

Latest released the research study on Global Investment Management Software Market, offers a detailed overview of the factors influencing the global business scope. Investment Management Software Market research report shows the latest market insights, current situation analysis with upcoming trends and breakdown of the products and services. The report provides key statistics on the market status, size, share, growth factors of the Investment Management Software The study covers emerging player’s data, including: competitive landscape, sales, revenue and global market share of top manufacturers are EFront Financial Solutions (France), Quant IX Software (United States), Broadridge Investment Accounting (United States), Portfolio Shop (United States), Beiley Software Inc. (United States), Quicken Inc. (United States), OneStream Software (United States), Finartis Group SA (Switzerland), QED Financial Systems (United States), Instream Solutions (United States)

Free Sample Report + All Related Graphs & Charts @: https://www.advancemarketanalytics.com/sample-report/14441-global-investment-management-software-market

Investment Management Software Market Definition:

Investment management software help to manage, recognize and communicate the risks and performance of investment and assets for financial advisors, investor and their clients. It provides on-demand access for the investments through an investor portal. Investment management software market has high growth prospects owing to increasing demand for the effective resource management system from various Industries and technological advancement for product development.

Market Drivers:

Provide Better Decision Making, Risk Management and Improves Operational Efficiency

Compatible with Numerous Platform Such As Windows. Mac, And Others

Market Opportunities:

Increasing Demand for Investment Management Software from Small and Medium Enterprises

Growing Adoption in Developing Economies for Auditable Asset and Compliance Management

Market Trend:

Emphasizing On Real-Time Investment Management Analytics

Increasing Demand for Effective Resource Management System

The Global Investment Management Software Market segments and Market Data Break Down are illuminated below:

by Application (Asset management, Wealth management, Sovereign wealth funds management, Pension funds management, Personal banking management, Insurance investment management, Others), Deployment Model (On-Premise, Cloud), End User (Commercial ( Small and Medium Enterprises, and Large Enterprises), Individuals)

Region Included are: North America, Europe, Asia Pacific, Oceania, South America, Middle East & Africa

Country Level Break-Up: United States, Canada, Mexico, Brazil, Argentina, Colombia, Chile, South Africa, Nigeria, Tunisia, Morocco, Germany, United Kingdom (UK), the Netherlands, Spain, Italy, Belgium, Austria, Turkey, Russia, France, Poland, Israel, United Arab Emirates, Qatar, Saudi Arabia, China, Japan, Taiwan, South Korea, Singapore, India, Australia and New Zealand etc.

Enquire for customization in Report @: https://www.advancemarketanalytics.com/enquiry-before-buy/14441-global-investment-management-software-market

Strategic Points Covered in Table of Content of Global Investment Management Software Market:

Chapter 1: Introduction, market driving force product Objective of Study and Research Scope the Investment Management Software market

Chapter 2: Exclusive Summary – the basic information of the Investment Management Software Market.

Chapter 3: Displayingthe Market Dynamics- Drivers, Trends and Challenges of the Investment Management Software

Chapter 4: Presenting the Investment Management Software Market Factor Analysis Porters Five Forces, Supply/Value Chain, PESTEL analysis, Market Entropy, Patent/Trademark Analysis.

Chapter 5: Displaying market size by Type, End User and Region 2015-2020

Chapter 6: Evaluating the leading manufacturers of the Investment Management Software market which consists of its Competitive Landscape, Peer Group Analysis, BCG Matrix & Company Profile

Chapter 7: To evaluate the market by segments, by countries and by manufacturers with revenue share and sales by key countries (2021-2026).

Chapter 8 & 9: Displaying the Appendix, Methodology and Data Source

Finally, Investment Management Software Market is a valuable source of guidance for individuals and companies in decision framework.

Data Sources & Methodology The primary sources involves the industry experts from the Global Investment Management Software Market including the management organizations, processing organizations, analytics service providers of the industry’s value chain. All primary sources were interviewed to gather and authenticate qualitative & quantitative information and determine the future prospects.

In the extensive primary research process undertaken for this study, the primary sources – Postal Surveys, telephone, Online & Face-to-Face Survey were considered to obtain and verify both qualitative and quantitative aspects of this research study. When it comes to secondary sources Company's Annual reports, press Releases, Websites, Investor Presentation, Conference Call transcripts, Webinar, Journals, Regulators, National Customs and Industry Associations were given primary weight-age.

For Early Buyers | Get Up to 20% Discount on This Premium Report: https://www.advancemarketanalytics.com/request-discount/14441-global-investment-management-software-market

What benefits does AMA research study is going to provide?

Latest industry influencing trends and development scenario

Open up New Markets

To Seize powerful market opportunities

Key decision in planning and to further expand market share

Identify Key Business Segments, Market proposition & Gap Analysis

Assisting in allocating marketing investments

Definitively, this report will give you an unmistakable perspective on every single reality of the market without a need to allude to some other research report or an information source. Our report will give all of you the realities about the past, present, and eventual fate of the concerned Market.

Thanks for reading this article; you can also get individual chapter wise section or region wise report version like North America, Europe or Southeast Asia.

Contact US:

Craig Francis (PR & Marketing Manager)

AMA Research & Media LLP

Unit No. 429, Parsonage Road Edison, NJ

New Jersey USA – 08837

[spacetimewithstuartgary]

Physicists embark on six-year hunt for dark matter particle

Aalto University researchers will probe the secrets of dark matter using a quantum detector of unprecedented sensitivity

In the pitch dark of the cosmos lurks an invisible kind of matter. Its presence is seen in the rippling ebb and flow of galaxies, but it’s never been directly observed. What secrets lie beneath the surface, brewing in the deep?

Physicists have long theorized about the composition of dark matter, which is thought to be five times more abundant than regular matter. Among competing hypotheses, one particle has emerged as a promising candidate: the axion.

Researchers at Aalto University are setting out on a six-year project to find evidence for the existence of axions. They will do so as part of a newly founded consortium called DarkQuantum, alongside researchers at the University of Zaragoza, who are coordinating the project, as well as researchers at the French National Centre for Scientific Research, Karlsruhe Institute of Technology, and other partner institutions.

This new consortium will be the first to use the latest quantum technologies to build sensors with unprecedented scanning sensitivity. DarkQuantum was awarded €12.9 million on October 26 by the European Research Council, of which roughly €2 million is set aside for Aalto University Senior Lecturer and Docent Sorin Paraoanu and his Superconducting Qubits and Circuit QED (KVANTTI) research group.

‘We are peering into a deep, dark pit. If it exists, the axion goes beyond the standard model of elementary particles,’ Paraoanu says. ‘Such an observation would be comparable in significance to the Higgs boson discovery in the early 2010s. But at least with the Higgs boson, they knew where to start looking!’

‘The nature of dark matter is one of the biggest mysteries in modern science,’ adds University of Zaragoza Professor Igor Garcia Irastorza, who also heads the DarkQuantum consortium. ‘If dark matter is made of axions, we have a real chance of detecting it with this project.’

Although there have been attempts to observe axions in the past, this latest endeavor will capitalize on quantum phenomena to enable researchers to better filter out noise and repeat their experiments with greater fidelity. That’s where Paraoanu and his team come in.

Moving mountains

Zoom into our small corner of the Milky Way galaxy, deep under the mountains spanning the border between Spain and France. This is the site of the Canfranc Underground Laboratory, which will house a high-frequency sensor the DarkQuantum researchers plan to build. The other, low-frequency sensor will be located at the German Electron Synchrotron (DESY) in Hamburg.

Paraoanu and his KVANTTI group are primarily responsible for building and tuning the high-frequency sensor, as well as writing the algorithms and software to use it. This sensor, called a haloscope, will probe the depths of the galactic halo in search of axions.

Putting the sensor deep underground helps eliminate cosmic background radiation, and it may offer a unique opportunity to simultaneously study certain noise-reduction techniques for quantum computing.

‘Our high-frequency sensor will be 10-100 times more sensitive than previous iterations, and it will be able to scan on the scale of a few microelectron volts. It will use superconducting qubits—the same qubits used in quantum computers—but they will serve in a different role as detectors in this haloscope,’ Paraoanu says.

Previous attempts to detect axions have used linear amplifiers, which tend to introduce noise and effectively absorb particles into the system. Paraoanu’s sensor will rely on quantum nondemolition measurements, which will allow for repeated experiments with the same particles.

‘The theory suggests that, in an ultra-cold environment, we can introduce a magnetic field that will cause any axions present to decay into photons. If we detect any photons in the cavity, then we can conclude that axions are present in the system, and that they do indeed exist,’ Paraoanu says.

Synergy Grant

The European Research Council’s Synergy Grant is prestigious, and Paraoanu and his team are only the second in Aalto University’s history to receive the grant—the first was awarded to Professor Risto Ilmoniemi for his ongoing ConnectToBrain project.

The six-year project will be broken into two parts: a four-year scaling up phase, which includes the construction, tuning and transportation of the haloscopes; and a two-year experimental phase, in which the team will gather data. Paraoanu expects to have openings for several researcher positions in the project in the coming years.

Other partner institutions named in the Synergy Grant include the Max Planck Society for the Advancement of the Sciences, the Polytechnic University of Cartagena, and the Spanish National Research Council.

Paraoanu and the KVANTTI research group will carry out their work using OtaNano equipment. OtaNano is Finland's national research infrastructure for micro-, nano-, and quantum technologies. Specifically, Paraoanu will perform his work at the Low Temperature Laboratory, founded by Finnish physicist Olli V. Lounasmaa. Paraoanu is also involved in InstituteQ and in the new Finnish Quantum Flagship (FQF).

IMAGE....Researchers will utilize quantum technologies to develop one of the world's most sensitive detectors ever built. CREDIT Mikko Raskinen/Aalto University

#science #space #astronomy #physics #astrophysics #DARK MATTER

[ailtrahq]

Sergey Nazarov, the creator of Chainlink, recently shared his thoughts on the potential for mass adoption of cryptocurrencies, particularly in the context of a failing banking system. Sergey Nazarov is best known as the co-founder of Chainlink Labs, where he has spent nearly four years helping to develop hybrid smart contracts. Before Chainlink, he co-founded SmartContract, a company that connects smart contracts to external data and bank payments. Nazarov also had a role in Secure Asset Exchange, a decentralized platform for real-time revenue sharing. Additionally, he was a General Partner at QED Capital, focusing on venture capital for tech teams in Russia and Eastern Europe. With experience in both venture capital and blockchain technology, Nazarov is a significant player in the cryptocurrency and smart contract sectors. According to a report by The Daily Hodl, in a recent interview on the Bankless podcast, Nazarov outlined two possible scenarios that could unfold for the crypto and blockchain sectors over the next decade. Nazarov presented two contrasting scenarios for the future of crypto. The first, which he calls the “slow case,” involves the crypto industry and its underlying technology continues to grow at their current pace. This gradual growth would slowly siphon value away from the traditional financial system. The second scenario, termed the “fast case” by Nazarov, is more dramatic. It envisions a rapid collapse of the traditional financial system, leading to widespread financial distress. This would force people to acknowledge the advantages of cryptographic money systems that offer verifiable transactions. In Nazarov’s “fast case” scenario, the collapse would be so severe that it couldn’t be mitigated by government intervention. Such a collapse would result in significant financial hardship for society, increased political tension, and international issues. Nazarov argues that this would make people realize the fragility of existing financial systems and make a cryptographically secure world highly appealing. He further elaborates that any entity not offering cryptographic guarantees for economic transactions would be at a disadvantage in such a world. According to Nazarov, not being part of this “verifiable web” would be akin to not being on the internet. Even if the “slow case” scenario plays out, Nazarov believes that the crypto industry is on a trajectory toward a $10 trillion market cap. He suggests that this path was set when the industry crossed the $200 billion mark. [embed]https://www.youtube.com/watch?v=AzQnY0CqHOw[/embed]

[delicatemagazinedreamer]

Bile Duct Cancer Market Is Estimated To Witness High Growth Owing To Rising Incidence of the Disease

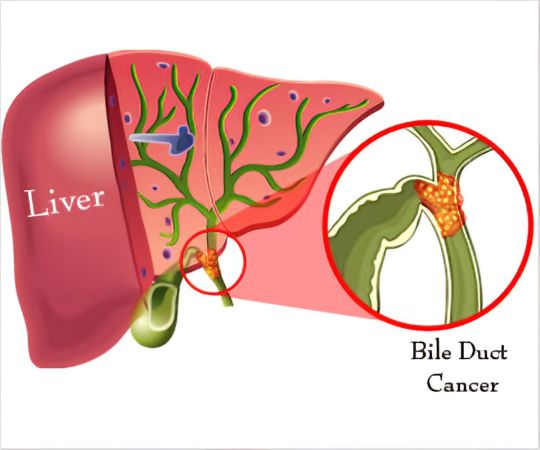
The global Bile Duct Cancer Market is estimated to be valued at US$ 185.4 million in 2021 and is expected to exhibit a CAGR of 12.8% over the forecast period 2021-2028, as highlighted in a new report published by Coherent Market Insights.

Market Overview Bile duct cancer, also known as cholangiocarcinoma, is a rare and aggressive form of cancer that affects the bile ducts, which are tubes that carry bile from the liver to the small intestine. The market for bile duct cancer treatment is driven by the rising incidence of the disease, which is mainly attributed to factors such as increasing prevalence of risk factors like chronic liver diseases, obesity, and exposure to certain chemicals. The need for effective treatment options for bile duct cancer has led to the development of novel therapies and targeted drugs. These advancements are expected to drive market growth in the coming years.

Market Key Trends One key trend in the Bile Duct Cancer market is the increasing adoption of targeted therapies. Targeted therapies are designed to specifically attack cancer cells or block the growth of tumors by targeting specific genes or proteins. These therapies have shown promising results in clinical trials and have been proven to be more effective than traditional chemotherapy in some cases. For example, QED Therapeutics, Inc. is developing infigratinib, a targeted therapy that inhibits the FGFR gene mutations commonly found in bile duct cancer. In a phase II clinical trial, infigratinib demonstrated a 75% overall response rate in patients with FGFR2 fusion-positive advanced cholangiocarcinoma.

PEST Analysis - Political: Government policies and regulations regarding cancer research and healthcare infrastructure can impact the availability and accessibility of treatments for bile duct cancer patients. - Economic: The economic conditions of a country can affect the affordability of treatments and the willingness of patients to seek medical care. - Social: Awareness campaigns and initiatives by healthcare organizations and patient advocacy groups play a crucial role in early diagnosis and treatment of bile duct cancer. - Technological: Advancements in diagnostic techniques, such as imaging technologies and biomarker analysis, can contribute to early detection and improved treatment outcomes for bile duct cancer. Key Takeaways - The global bile duct cancer market is expected to witness high growth, exhibiting a CAGR of 12.8% over the forecast period, due to the increasing incidence of the disease and the need for effective treatment options. - Asia Pacific is expected to be the fastest-growing region in the bile duct cancer market, driven by a large patient population, improving healthcare infrastructure, and rising investments in cancer research and development. - Key players operating in the global bile duct cancer market include Incyte Corporation, Eisai Co., Ltd., QED Therapeutics, Inc., Agios Pharmaceuticals, Inc., RenovoRx, Ability Pharmaceuticals, Imbrium Therapeutics L.P., and Delcath Systems, Inc. These companies are actively involved in research and development activities and strategic collaborations to develop innovative therapies for bile duct cancer. In conclusion, the bile duct cancer market is witnessing significant growth due to the rising incidence of the disease and the development of targeted therapies. With increasing awareness, advancements in technology, and investments in cancer research, the market is expected to provide lucrative opportunities for key players in the coming years.

#Bile Duct Cancer #Bile Duct Cancer Market #Bile Duct Cancer Market Size #Bile Duct Cancer Market Share #Bile Duct Cancer Market Growth #Pharmaceutical