#hubble constant is the rate at which the universe is expanding. we don't know what it is because different methods produce different

[sagesilentfire]

Physicists Discovers Difference In Hubble Constant Actually Error in Entering Numbers Into a Calculator

"My bad," says the scientist responsible.

"Oh, that makes sense," said every single scientist and astronomy geek ever, before burning them alive.

Reports say general public confused, wondering what the Hubble constant is and why it's important.

#i will continue to post niche memes none of my followers followed me for or understand #hubble constant is the rate at which the universe is expanding. we don't know what it is because different methods produce different #results. but it is extremely important to understanding the universe #i am a physics major #physics #astronomy #the joke is #of course #that entering things into a calculator sucks #i hate it #i got a new calculator and i hate it so much #so much #theoretical physics #mathematics #chemistry #because that's where the new calculator is from #science #math jokes #queue queue

[oflgtfol]

@colorofitall asked: How much is the universe expanding these days?

Short answer:

Current estimates of the expansion rate hover around ~70 (km/s)/Mpc. That's a weird unit, but you can think of it as the universe is expanding at a rate of ~70 km/s for every 1 Mpc (1 Mpc is about 3.26 million light years).

Long answer:

We don't really know!

The universe is not really expanding at a constant speed in the first place. In 1998, astronomers discovered that the rate of expansion is accelerating - meaning, that the speed of expansion is increasing over time.

So we measure the rate of expansion in terms of the Hubble parameter, H. And because the expansion rate is always changing due to acceleration, the Hubble parameter is time-dependent. The current rate of expansion is constant and represented by H0.

The Hubble parameter was named after Edwin Hubble who discovered that the universe is expanding way back in the 1920s, and he discovered this by observing the redshift of different galaxies.

It's easiest to think of redshift in terms of the Doppler effect. In case you aren't familiar with it, think of it in terms of like, a car driving down the street. As the car approaches you, the sound waves it emits get compressed in front of it as it moves. Because the waves get squeezed together, the frequency increases, which we hear as a higher pitched sound. As the car moves away, the sound waves spread out and have a lower frequency, and so we hear a lower pitch.

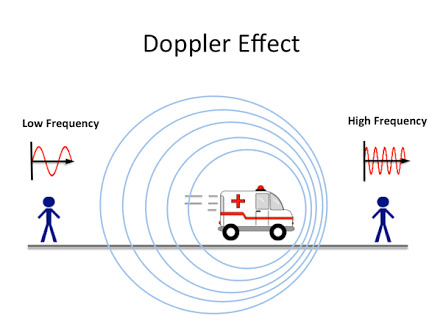
Because light travels as a wave, it also experiences this phenomenon! So when an object moves towards us, the light shifts to a higher frequency, towards the blue end of the visible spectrum. This is called blueshift. Likewise, when an object moves away from us, the frequency decreases, and we observe redshift.

So Hubble saw that pretty much every galaxy he looked at was redshifted. And the kicker is that the galaxies further away from us were even more redshifted. This means that everything is moving away from us, and that objects already far away are moving away even faster. The only logical conclusion to explain this? The universe must be expanding, with the space itself between each object getting stretched out.

And so, using these observations, he defined what we now call Hubble's law: v = H0 * d, where v is the object's velocity we observe due to expansion, H0 is Hubble's constant which measures the expansion rate, and d is the distance between the observer and the object.

(It's important to note that Hubble was not the only one involved in this discovery! For like, at least a decade before he published his results, there had been people working out the math, and he was not the first one to propose that the universe is expanding. But he is widely accredited for it because he made the breakthrough with relating velocity and distance together in Hubble's law.)

So how can we find H0?

The easiest way is to think of it is in terms of Hubble's law. All we really need is the velocity of a distant object and its distance from Earth. Seems simple enough, right?

If we observe many objects (stars, supernovae, galaxies, etc.) at various distances and measure their redshift, then we can figure out the value of H0. This method is looking into the "late" universe - aka, relatively close to "right now." (I say relatively because it takes time for the light to reach us, so we are observing in real time something that actually happened hundreds to thousands to even millions of years ago.) Various studies like these have been done in the past few decades, giving a Hubble constant of 72, 73, 74 (km/s)/Mpc. All within a reasonable margin of error of each other, pretty swell!

But we can peer back into the "early" universe as well. Objects that are so far away that their light is only just reaching us, and so they appear to us as they were at the very early years of the universe. The very earliest thing that we can observe is the Cosmic Microwave Background (CMB), radiation left over from the Big Bang that has been redshifted so much that it is in now in the microwave spectrum.

Think of it like a temperature map: blue is cold, red is hot. Red represents area of high density, while blue represents voids. These very small temperature fluctuations in the CMB represent structures that would evolve as the universe aged - large structures that we see now as galaxies and galaxy clusters. If we trace those disturbances through time, we can measure H0 again.

The earliest studies done this way agreed with previous estimates, hovering around 70, 72 (km/s)/Mpc. This was good news, and exactly what scientists expected.

... But then more studies were done, became more precise, and the value started dropping to about 67 and 68 (km/s)/Mpc, and their uncertainties no longer overlapped with late universe estimates.

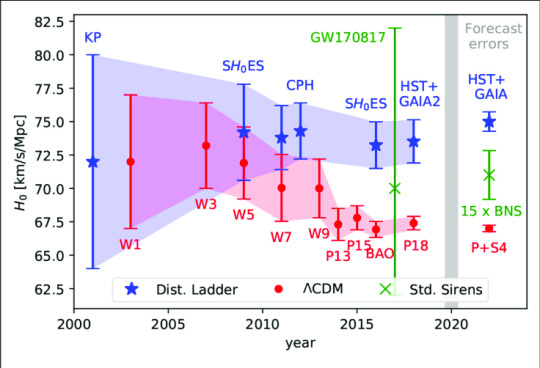
Here's a graph of the different estimates from studies done over the years. The red ones were measured using the CMB, and the blue ones were measured using late universe objects. As you can see, the gap is widening between the two methods, even as they become more precise (seen by narrower error bars).

(A bit of a side-note, but the first green one actually comes from gravitational wave observations, done in this LIGO collaboration from 2017 which I think is really neat!!)

All of this is a huuuge problem in cosmology right now. It's even got a name: the Hubble tension. It shouldn't matter at all which method we use, the value should agree, so why aren't we seeing this? Is there something wrong with our math? Our measurements? Or is our model of the universe itself flawed somehow?

In my astronomy class we always used 70 km/s/Mpc as the value of H0. And in a way it's pretty much the average value between 67 and 73. So for a short answer, yes the expansion rate is about roughly ~70 (km/s)/Mpc, and it works fine for normal math. But in terms of like, accurately understanding the universe and delving deeeep into theoretical cosmology that relies heavily on a precise value of H0, it is Not Fine. Frankly we really don't know yet and it's an exciting area of research still!!!

#welcome to this episode Brot Actually Types Like A Normal Person #brot posts #astro posting #this took a while lol #thank youuu for letting me ramble :D