#ضرب_تانسوری

[mthmtc]

حاصل ضرب تانسوری (۲- ضرب و پیچش)

پست جدید انتشار یافت https://mthmtcs.ir/tensor-product-2/

حاصل ضرب تانسوری (۲- ضرب و پیچش)

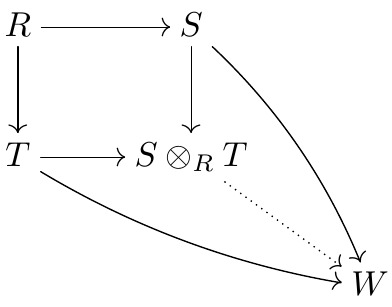
هنگاهی که $E$ و $F$ جبر می باشند می توان ضربی روی $E\odot F$ تعریف کرد با این خاصیت که برای هر $e_1, e_2\in E$ و $f_1, f_2\in F$ داریم $(e_1\otimes f_1)(e_2\otimes f_2):=e_1e_2\otimes f_1f_2$. برای تعریف چنین ضربی بصورت زیر عمل می کنیم. ابتدا برای هر $e\in E$ و $f\in F$ ثابت، نگاشت دوخطی $\psi_e,f:E\times F\To E\odot F$ تعریف شده بصورت $\psi_e,f:(g,h)\mapsto eg\otimes fh$ را در نظر می گیریم با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفردی مانند $\varphi_e,f:E\odot F\To E\odot F$ وجود دارد بطوریکه $\varphi_e,f\circ\pi=\psi_e,f$. حال نگاشت دوخطی $\varphi:E\times F\To \rm Hom(E\odot F)$ را به صورت $\varphi:(e,f)\mapsto\varphi_e,f$ تعریف می کنیم دوباره با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفردی مانند $\mu:E\odot F\To E\odot F$ وجود دارد بطوریکه $\mu\circ\pi=\varphi$ و \beginalign* \mu(\sum e_i\otimes f_i)(\sum g_j\otimes h_j)&=\sum\varphi(e_i,f_i)(\sum g_j\otimes h_j)\cr &=\sum\varphi_e_i,f_i(\sum g_j\otimes h_j)=\sum\sum e_ig_j\otimes f_ih_j \endalign* حال عمل ضرب بین دو عنصر $s,t\in E\odot F$ را $t\cdot s:=\mu(t)(s)$ تعریف می کنیم و $E\odot F$ تبدیل به یک جبر می شود. فضای برداری مزدوج، فضای برداری $V$ را با $V^c$ نمایش می دهیم. بنابراین $V$ با $V^c$ به عنوان گروه آبلی یکی هستند اما ضرب اسکالر روی $V^c$ به صورت $(\lambda,\upsilon)\mapsto\bar\lambda\upsilon$ تعریف می شود. اگر $V$ و $W$ فضاهای برداری مختلط باشند و $T:V\To W$ نگاشتی خطی و $S:V\To W$ نگاشتی مزدوج خطی باشد آنگاه نگاشتهای $T:V\To W^c$، $ T:V^c \To W $، $ S: V^c \To W^c $ خطی مزدوج و $T:V^c\To W^c$، $S:V\To W^c$، $S:V^c\To W$ خطی می باشند. اگر $E$ و $F$ $*$-جبر باشند می توان یک پیچش روی $E\odot F$ وابسته به پیچشهای که روی $E$ و $F$ وجود دارد، تعریف کرد. فرض کنیم $\frak s:E\times F\To (E\odot F)^c$ نگاشت دوخطی تعریف شده به صورت $\frak s:(e,f)\mapsto e^*\otimes f^*$ باشد بنابر گزاره ۲٫۱ نگاشت یکتای $*:E\odot F\To (E\odot F)^c$ بطوریکه $*\circ\pi=\frak s$. یعنی \beginalign* (\sum e_i\otimes f_i)^*=\sum e_i^*\otimes f_i^* \endalign*

گزاره ۵٫۱ : فرض کنید $B\:,\:A$ و $C$ جبر باشند. اگر $\psi:A\times B\To C$ نگاشت خطی ضربی ( یعنی $\psi(aa^\prime,bb^\prime)=\psi(a,b)\psi(a^\prime,b^\prime)$ ) باشد. آنگاه $\psi$ بطوریکتا به نگاشت خطی ضربی $\varphi:A\odot B\To C$ توسیع می یابد. اگر $\psi$ حافظ پیچش باشد، آنگاه $\varphi$ نیز چنین است.

اثبات: با استفاده از گزاره ۲٫۱ نگاشت خطی یکتای $\varphi:A\odot B\To C$ بطوریکه $\varphi\circ\pi=\psi$. لذا $\varphi(\sum a_i\otimes b_i)=\sum\psi(e_i,b_i)$. حال چون $\varphi$ خطی می باشد، کافی است ثابت کنیم \beginalign* \varphi((a_1\otimes b_1)(a_2\otimes b_2))&=\varphi(a_1a_2\otimes b_1b_2)\cr &=\psi(a_1a_2,b_1b_2)\cr &=\psi(a_1,b_1)\psi(a_2,b_2)\cr &=\varphi(a_1\otimes b_1)\varphi(a_2\otimes b_2) \endalign* لذا $\varphi$ ضربی می باشد. حال اگر $\psi$ حافظ پیچش باشد، دوباره با استفاده از خاصیت خطی $\varphi$ داریم $\varphi(a^*\otimes b^*)=\psi(a^*,b^*)=\psi(a,b)^*=\varphi(a\otimes b)^*$ و در نتیجه $\varphi$ حافظ پیچش می باشد. $\square$

با استفاده از گزاره های ۲٫۱ و ۵٫۱ نتایج مهم زیر را داریم

اگر $\psi_E:E\To G$ و $\psi_F:F\To H$ نگاشتهای خطی باشند، آنگاه $\psi_E\odot\psi_F:E\odot F\To G\odot H$ را نگاشت خطی تعریف شده به صورت $\psi_E\odot\psi_F:e\otimes f\mapsto \psi(e)\otimes\psi(f)$ در نظر می گیریم که توسیع نگاشت دوخطی $(e,f)\mapsto \psi(e)\otimes\psi(f)$ می باشد. اگر در فضاهای زمینه ضرب تعریف شده باشد و $\psi_E,\psi_F$ ضربی باشند آنگاه $\psi_E\odot\psi_F$ نیز ضربی خواهد بود.

اگر $\varphi_E:E\To G$ و $\varphi_F:F\To G$ نگاشتهای خطی و $G$ جبر باشد، آنگاه $\varphi_E\odot\varphi_F:E\odot F\To G$ را نگاشت تعریف شده به صورت $\varphi_E\odot\varphi_F:e\otimes f\mapsto \varphi_E(e)\,.\,\varphi_F(f)$ در نظر می گیریم که توسیع نگاشت دوخطی $(e,f)\mapsto \varphi_E(e)\,.\,\varphi_F(f)$ می باشد. اگر $E$ و $F$ جبر باشند و $\varphi_E,\varphi_F$ ضربی و جابجا (یعنی $\varphi_E(e)\varphi_F(f)=\varphi_F(f)\varphi_E(e)$) شوند، آنگاه $\varphi_E\odot\varphi_F$ نیز ضربی می باشند.

در مثالهای بالا با استفاده از نگاشتهای خطی روی فضاها، نگاشتهایی خطی روی ضرب تانسوری این فضاها تعریف کردیم. عکس این سوال نیز مهم است. یعنی آیا برای نگاشت $\xi:E\odot F\To G$، نگاشتهای $\varphi_E:E\To G$ و $\varphi_F:F\To G$ وجود دارد بطوریکه $\varphi_E\odot\varphi_F=\xi$. هنگامی که $\varphi_E$ و $\varphi_F$ وجود داشته باشند آنها را تحدید $\xi$ خوانیم.

مثال ۱٫۱ :

$A\simeq A\odot \Bbb C$ . فرض کنیم نگاشت خطی $\varphi:\sum a_k\otimes\lambda_k\mapsto \sum\lambda_k a_k$ از $A\odot\Bbb C$ بتوی $A$ توسیع نگاشت دوخطی $(a,\lambda)\mapsto \lambda a$ از $A\times\Bbb C$ به $A$ باشد. بوضوح $\varphi$ پوشا و یک به یک می باشد. اگر $A$ جبر (با پیچش) باشد آنگاه $\varphi$ ضربی (حافظ پیچش) می باشد.

جبرهای ماتریسی: $A\odot\Bbb M_n(\Bbb C)\simeq\Bbb M_n(A)$ ماتریسهای $n\times n$ با ۱ در درایه با سطر $i$ و ستون $j$ و بقیه درایه ها صفر. لذا هر عضو $A\odot \Bbb M_n$ را می توان بطور منحصر بفرد به صورت \beginalign* t=\sum a_i j\otimes e_i j \endalign* نوشت. حال نگاشت $\psi:A\odot\Bbb M_n(\Bbb C)\To \Bbb M_n(A)$ تعریف شده بصورت $\psi:\sum a_i j\otimes e_i j\mapsto (a_i j)$ خطی و ضربی ($e_i j\cdot e_km=\delta_j k\cdot e_i m$) و حافظ پیچش ($e_i j^*=e_j i$) می باشد و آشکارا دوسویی نیز می باشد.

نشاندن به عنوان زیرمجموعه چگال: $C_0(X)\odot A\hookrightarrow C_0(X\rightarrow A)$ که $X$ فضای موضعاً فشرده و $A$ $C^*$-جبر می باشد. فرض کنیم نگاشت خطی $\varphi:C_0(X)\odot A\To C_0(X\rightarrow A)$ توسیع نگاشت دوخطی $\psi:C_0(x)\times A\To C_0(X\rightarrow A)$ تعریف شده به صورت $\psi:(f,a)\mapsto \psi_(f,a)$ که $\psi_(f,a)(x)=f(x)a$ اشد. واضح است که $\psi_(f,a)\in C_0(X\rightarrow A)$. حال ثابت می کنیم که $\varphi$ یک به یک می باشد. فرض کنیم $\a_j\_J$ پایه ای برای $A$ باشد. پس می توان هر عضو $C_0(X)\odot $ را بطور یکتا به صورت $\sum f_j\otimes a_j$ نوشت. حال فرض کنیم $\varphi(\sum f_j\otimes a_j)=0$ لذا $\sum\psi_(f_j,a_j)=0$ و در نتیجه برای هر $x\in X$ داریم $\sum\psi_(f_j.a_j)(x)=\sum f_j(x)a_j=0$ و در نتیجه برای هر $x\in X$ و هر $j$ داریم $f_j(x)=0$ و $f_j\equiv 0$ پس $\sum f_j\otimes a_j=0$ و $\varphi$ یک به یک می باشد. حال نشان می دهیم که $C_0(X)\odot A$ در $C_0(X\rightarrow A)$ چگال می باشد. فرض کنیم $f\in C_0(X\rightarrow A)\ ,\ 0 \beginalign* \cal O_x:=\\ f_0(x)\ -\ f_0(y)\ \ \endalign* چون $X_0$ فشرده می باشد لذا این پوشش دارای زیر پوشش متناهی می باشد. پس $x_1,\ldots,x_n$ وجود دارد بطوریکه $X_0\subseteq\cup_i=1^n \cal O_x_i $ . با استفاده از قضیه افراز واحد ((گزاره ۴۱.۴ کتاب آنالیز حقیقی فولند)) روی $X_0$ داریم: توابع $g_x_i\in C_0(X\rightarrow [0,1])$ وجود دارد بطوریکه $g_x_i|X_0\backslash\cal O_x_i=0$ و $\sum g_x_i=1$ روی $X_0$ و $۰\leq\sum g_x_i\leq 1$ روی $X\backslash X_0$ . فرض کنیم $g:=\sum g_x_i\otimes f(x_i)$ پس $g\in C_0(X)\odot A$ و $\varphi(g)$ تقریبی از $f_0$ و لذا تقریبی از $f$ می باشد.

#real analysis #real_analysis #tensor #tensor_product #آنالیز_حقیقی #تانسور #جبری #ریاضیات #ضرب_تانسوری #فضای_برداری

[mthmtc]

حاصل ضرب تانسوری (۱-فضاهای برداری)

پست جدید انتشار یافت https://mthmtcs.ir/tensor-product-1/

حاصل ضرب تانسوری (۱-فضاهای برداری)

گزاره ۱٫۱ : فرض کنید $G_1,F,E$ و $G_2$ فضاهای برداری و \beginalign* \pi_2 : E \times F \To G_2 \quad , \quad \pi_1 : E \times F \To G_1 \endalign* نگاشتهای دوخطی باشند.اگر برای هر فضای برداری $M$ وهر نگاشت دوخطی $ \chi : E \times F \To M $ نگاشتهای خطی منحصر به فرد \beginalign* \eta_2 : G_2 \To M \qquad , \qquad \eta_1 : G_1 \To M \endalign* وجود داشته باشد بطوریکه $ \eta_2 \! \circ \pi_2 =\chi $ و $ \eta_1 \! \circ \pi_1 =\chi $، آنگاه یک ایزومرفیسم مانند $ \varphi : G_1 \To G_2 $ وجود دارد بطوریکه $ \varphi \circ \pi_1 = \pi_2 $ .

اثبات: ابتدا فرض کنیم $ M = G_2 $ و $ \chi = \pi_2 $ آنگاه بنابر فرض $ \psi_1 : G_1 \To M = G_2 $ بطوریکه $ \psi_1 \circ \pi_1 = \pi_2 $. حال $ M = G_1 $   و $ \chi = \pi_1 $ آنگاه بنابر فرض $ \psi_2 : G_2 \To M = G_1 $ بطوریکه $ \psi_2 \circ \pi_2 = \pi_1 $.  با ترکیب دو رابطه بالا داریم \beginalign* (\psi_1 \circ \psi_2) \circ \pi_1 = \pi_2 \qquad , \qquad (\psi_2 \circ \psi_1) \circ \pi_1 = \pi_1 \endalign* حال چون $ \rm id_G_1 \circ \pi_1 = \pi_1 $ و $ \rm id_G_2 \circ \pi_2 = \pi_2 $ تجزیه های دیگری از این نوع می باشند. لذا بنابر یکتایی تجزیه داریم: \beginalign* \psi_1 \circ \psi_2 = \rm id_G_2 \qquad , \qquad \psi_2 \circ \psi_1 = \rm id_G_1 \endalign* و در نتیجه $ \psi_1 $ یک به یک و پو شا می باشد و $ \psi_1 \circ \pi_1 = \pi_2 $ . در نتیجه $ \varphi = \psi_1 $ و اثبات کامل می شود. $\blacksquare$

نکته ۱٫۱ : با توجه به اثبات گزاره ۱٫۱ شرط یکتایی تجزیه اساسی می باشد. با این حال هنگامی که نگاشتهای $\pi_1$ و $\pi_2$ پوشا هستند و یا بردشان به ترتیب $ G_1 $ و $ G_2 $ را تولید می کند تجزیه یکتاست. فرض کنیم $ \chi : E\times F \To M $ نگاشت دوخطی باشد و $ \beta : G_1 \To M $ و $ \beta’ : G_1 \To M $ دو تجزیه مختلف برای $ \chi $ باشند یعنی $ \beta \circ \pi_1 = \chi $ و $ \beta’ \circ \pi_1 = \chi $. اگر هر $ g \in G_1 $ را بتوان به صورت $ g= \sum \pi_1 (e_i,f_i) $ آنگاه $ \chi =\beta \circ \pi_1 =\beta’ \circ \pi_1 $ نتیجه می دهد که \beginalign* \beta (g) &= \beta \left( \sum \pi_1 (e_i,f_i) \right) = \sum \chi(e_i,f_i)\cr &= \sum \beta'(\pi_1 (e_i,f_i)) = \beta’ \left( \sum \pi_1(e_i,f_i) \right) = \beta'(g) \endalign* لذا  $ \beta = \beta’ $.

ساختار ضرب تانسوری جبری

فرض کنیم $E$ و $F$ فضای برداری باشند

  در حالت کلی $X^(Y)$ مجموعه تمام نگاشتهای از $Y$ بتوی $X$ می باشند بطوریکه دارای برد متناهی هستند. اعمال روی $\Bbb C^(E \times F)$ را به صورت زیر تعریف می کنیم : \beginalign* \sum\lambda(e,f)+\sum\mu(e,f)=\sum(\lambda+\mu)(e,f) \endalign* \beginalign* \mu\sum\lambda(e,f)=\sum(\mu\lambda)(e,f) \endalign* بااین اعمال $\Bbb C^(E \times F)$ به فضای برداری روی $\Bbb C$ با پایهٔ $E\times F$ تبدیل می شود. حال زیر فضای برداری تولید شده توسط عناصر زیر را $ \calN $ می نامیم \beginalign* (e_1+e_2,f)-(e_1,f)-(e_2,f) \endalign* \beginalign* (e,f_1+f_2)-(e,f_1)-(e,f_2) \endalign* \beginalign* \lambda(e,f)-(\lambda e,f)\quad \mboxو\quad \lambda(e,f)-(e,\lambda f) \endalign* که $ e,e_1,e_2 \in E ,\ f,f_1,f_2 \in F $ و $ \lambda \in \Bbb C $ . حال ضرب تانسوری جبری $E$ و $F$ را فضای خارج قسمتی \beginalign*E \odot F := \Bbb C^(E \times F)/ \cal N \endalign* تعریف می کنیم. حال اگر $\pi$ نگاشت خارج قسمتی از $\Bbb C^(E\times F)$ بروی $E\odot F$ باشد آنگاه چون \beginalign* \lambda(e,f)-(\lambda e,f)\in\cal N\quad \mboxو\quad (e_1+e_2,f)-(e_1,f)-(e_2,f)\in\cal N \endalign* \beginalign* \lambda(e,f)-(e,\lambda f)\in\cal N\quad \mboxو\quad (e,f_1+f_2)-(e,f_1)-(e,f_2)\in\cal N \endalign* داریم \beginalign* \pi(\lambda e_1+e_2,f)=\lambda\pi(e_1,f)+\pi(e_1,f) \endalign* \beginalign* \pi(e,\lambda f_1+f_2)=\lambda\pi(e,f_1)+\pi(e,f_2) \endalign* لذا تحدید $\pi$ بروی $E\times F$ دوخطی می باشد. عناصر $\pi(e,f)\in E\odot F$ که $e\in E,\ f\in F$ را عناصر ابتدایی می نامیم و با $e\otimes f$ نمایش می دهیم. چون $\pi$ پوشا می باشد هر عضو $t$ در $E\odot F$ را می توان به صورت مجموع متناهی از عناصر ابتدایی نوشت. \beginalign* t= \sum_i=1^N e_i\otimes f_i \endalign* اما این مجموع یکتا نیست چون $\pi$ یک به یک نیست. با توجه به ساختار $E\odot F$ داریم \beginalign* (e_1+e_2)\otimes f=e_1\otimes f+e_2\otimes f \endalign* \beginalign* e\otimes(f_1+f_2)=e\otimes f_1+e\otimes f_2 \endalign* \beginalign* \lambda(e\otimes f)=\lambda e\otimes f=e\otimes \lambda f \endalign* از روابط بالا آشکار است که برای هر $e\in E,\ f\in F$ داریم \beginalign* ۰=۰\otimes 0=0\otimes f=e\otimes 0 \endalign*

گزاره ۲٫۱ : فرض کنید $F,E$ فضای برداری و $\pi:E\times F\To E\odot F$ نگاشت دوخطی کانونی باشد.اگر $M$ یک فضای برداری و $\psi:E\times F\To M$ نگاشت دوخطی باشد آنگاه $\psi$ بطوریکتا روی $E\odot F$ توسیع می یابد یعنی نگاشت خطی یکتای $\varphi:E\odot F\To M$ وجود دارد بطوریکه $\varphi\circ\pi=\psi$.

اثبات: ابتدا $\psi$ را با استفاده از خاصیت خطی به نگاشت خطی $\tilde\psi :\mathbb C^(E\times F)\To M$ بصورت زیر توسیع می دهیم \beginalign*\tilde\psi \left(\sum\lambda(e,f)\right)=\sum\lambda\psi(e,f),\qquad e\in E,\ f\in F,\ \lambda\in\mathbb C \endalign* با توجه به خواص خطی $ \psi $ واضح است که $ \tilde\psi(\mathcal N)=0 $. حال نگاشت $ \varphi:E\odot F\To M $ را به صورت زیر تعریف می کنیم. فرض کنیم $ t\in E\odot F $ پس $ x\in \mathbb C^(E\times F) $ وجود دارد بطوریکه $ \pi(x)=t $ قرار می دهیم $ \varphi(t)=\tilde\psi(x)$. حال چون $ \tilde\psi(\mathcal N)=0 $ ، اگر $ t_1 , t_2 \in E\odot F $ و $ t_1=t_2 $ لذا $ t_1-t_2\in\mathcal N $ و در نتیجه $ \tilde\psi(t_1-t_2)=0 $ و $ \varphi(t_1)=\varphi(t_2) $ . لذا $ \varphi $ خوشتعریف است. فرض کنیم $ \gamma\in\mathbb C\ ,\ t_1=\pi(\sum\lambda(e,f))\in E\odot F\ ,\ t_2=\pi(\sum\mu(e,f))\in E\odot F $ پس \beginalign* \varphi(\gamma t_1+t_2)&=\varphi(\gamma(\pi(\sum\lambda(e,f)))+\pi(\sum\mu(e,f)))\\ &=\varphi(\pi(\sum(\gamma\lambda+\mu)(e,f))= \tilde\psi(\sum(\gamma\lambda+\mu)(e,f))\\ &=\tilde\psi(\sum(\gamma\lambda(e,f))+ \tilde\psi(\sum\mu(e,f))= \gamma(\tilde\psi(\sum\lambda(e,f)))+\tilde\psi(\sum\mu(e,f))\\ &=\gamma(\varphi(\pi(\sum\lambda(e,f))))+ \varphi(\pi(\sum\mu(e,f)))\\ &=\gamma(\varphi(t_1))+\varphi(t_2) \endalign* لذا $ \varphi $ خطی می باشد و داریم $ \varphi\circ\pi(e,f)=\psi(e,f)$. $\blacksquare$

نکته ۲٫۱ : بنابر گزاره بالا می توان گفت $E\odot F$ فضای برداری یکتای است بطوریکه برای هر فضای برداری $ M $ داریم \beginalign* \rm\bf Bil(E\times F ,\ M)\simeq\rm\bf Lin(E\odot F ,\ M) \endalign* توجه داریم که پیوستگی $ \psi $ پیوستگی $ \varphi $ را ایجاب نمی کند حتی اگر $ \pi $ پیوسته باشد. ما این مطلب را بعداً مورد بررسی قرار می دهیم.

گزاره ۳٫۱ : اگر $ \ e_j \_\mathcal J $ پایه‌ای برای $ E $ و $ \ f_k \_\mathcal K $ پایه‌ای برای $ F $ باشد. آنگاه $ \e_j\otimes f_k\_\mathcal J\times\mathcal K $ پایه‌ای برای $ E\odot F $ می باشد و $ \rm dim(E\odot F)=\rm dim(E)\rm dim(F) $ . علاوه بر این داریم \beginalign* E^(\mathcal K)\simeq E\odot F\simeq F\odot E \quad\mboxو\quad E\odot(F\odot G)\simeq(E\odot F)\odot G \endalign* که $ E^(\mathcal K) $ فضای تمامی نگاشتها از $\mathcal K $ بتوی $ E $ با برد متناهی می باشند.

اثبات: فرض کنیم $ G_1:=E\odot F $ و $ G_2:=E^(\mathcal K) $ . گزاره ۱٫۱ را بکار می بریم و ثابت می کنیم که $ G_1\simeq G_2 $ . نگاشتهای دوخطی $ \pi_1:E\times F\To G_1 $ و $ \pi_2:E\times F\To G_2 $ بصورت زیر تعریف می کنیم \beginalign* \pi_1:(e,f)\mapsto e\otimes f\ ,\quad \pi_2:(e,\sum_k\in\mathcal K\lambda_kf_k )\mapsto(\lambda_ke)_k\in\mathcal K \endalign* توجه داریم که $ G_1 $ و $ G_2 $ توسط برد نگاشتهای $ \pi_1 $ و $ \pi_2 $ تولید می شود. مجموعهٔ \beginalign* \\ \pi_2(e_j,f_k)=(\delta_k i\,e_j)_i\in\mathcal K\ ;\ (j,k)\in \mathcal J\times K\ \ \endalign* پایه‌ای برای $ E^(\mathcal K) $ می باشد. فرض کنید $ \chi $ نگاشتی دو خطی از $ E\times F $ به توی فضای برداری $ M $ باشد. با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفرد $ \eta_1:E\odot F\To M $ بطوریکه $ \eta_1\circ\pi_1=\chi $. حال نگاشت $ \eta_2:E^(\mathcal K)\To M $ را به صورت زیر تعریف می کنیم \beginalign* \eta_2((e_k)_\mathcal K):=\sum_\mathcal K \chi(e_k,f_k) \endalign* چون $ \chi $ دوخطی می باشد لذا $ \eta_2 $ خطی می باشد و داریم \beginalign* \eta_2\circ\pi_2(e,\sum_\mathcal K\lambda_kf_k)=\eta_2((\lambda_ke)_\mathcal K)=\sum_\mathcal K\chi(\lambda_ke,f_k)=\chi(e,\sum_\mathcal K\lambda_kf_k) \endalign* پس $ \eta_2\circ\pi_2=\chi $. و با استفاده از گزاره ۱٫۱ نتیجه می شود که $ E\odot F\simeq E^(\mathcal K) $ و یک ایزومرفیسم $ \varphi:E\odot F\To E^(\mathcal K) $ بطوریکه $ \varphi\circ\pi_1=\pi_2 $. بویژه $ \varphi(e_j\otimes f_k)=\pi_2(e_j,f_k) $ و در نتیجه مجموعهٔ \beginalign* \ e_j \otimes f_k\ ;\ (e_j,f_k)\in\mathcal J\times K \=\varphi^-1 \ \pi_2 (e_j,f_k)\ ;\ (j,k)\in\mathcal J\times K \ \endalign* که تصویر ایزومرفیک پایه‌ای از $ E^(\mathcal K) $ می باشد، پایه‌ای برای $ E\odot F $ می باشد. حال نگاشت خطی القا شده توسط نگاشت دوخطی $ (e,f)\mapsto f\otimes e $ را در نظر می گیریم واضح است که $ \phi $ ایزومرفیسم می باشد چون پایه را به پایه می برد و لذا $ E\odot F\simeq F\odot E $. بطور مشابه نگاشت $ \phi:(e,f\otimes g)\mapsto (e\otimes f)\otimes g $ از $ E\times(F\odot G) $ بتوی $ (E\odot F)\odot G $ دوخطی می باشد زیرا \beginalign* \phi((\lambda e_1+e_2),f\otimes g)&=((\lambda e_1+e_2)\otimes f)\otimes g\cr &=(\lambda(e_1\otimes f))\otimes g+(e_2\otimes f)\otimes g\cr &=\lambda\phi((e_1,f\otimes G))+\phi((e_2,f\otimes G)) \endalign* \beginalign* \phi(e,\lambda(f_1\otimes g_1)+f_2\otimes g_2)=\lambda\phi(e,f_1\otimes g_1)+\phi(e,f_2\otimes g_2) \endalign* حال نگاشت القا شده توسط $ \phi $ درنظر می گیریم که یک ایزومرفیسم از $ E\odot (F\odot G) $ به $ (E\odot F)\odot G $ می باشد. $\blacksquare$

از گزاره بالا داریم $ E\odot F $ و $ F\odot E $ بطورجبری ایزومرفیسم می باشند اما نرمهای نامتقارنی وجود دارند که $ E\odot F $ و $ F\odot E $ را تبدیل به فضاهای نرمدار متفاوتی می کند.

گزاره ۴٫۱ : فرض کنیم $ f_1,f_2,\dots,f_N\in F $ مستقل خطی باشند. اگر $ e_1,e_2,\dots,e_N\in E $ و $ \sum_i=1^Ne_i\otimes f_i=0$ آنگاه $ e_1=e_2=\cdots=e_N=0 $. بویژه اگر $ \f_k\_K $ پایه ای برای $F$ باشد آنگاه هر $ t\in E\odot F $ نمایش منحصر به فرد $ \sum_Ne_k\otimes f_k $ (مجموع متناهی) دارد.

اثبات: فرض کنیم $ \ \mathfrak e_1,\mathfrak e_2,\dots,\mathfrak e_n \ $ پایه ای برای $ \mathfrak E :=\rm Span\e_1,e_2,\dots,e_N\ $ واضح است که $ n\leqslant N $ و $ \\mathfrak e_\,l\_L $ توسیع $ \\mathfrake_1,e_2,\dots,e_n\ $ به پایه ای برای $ E $ باشد و $ \f_k\_K $ توسیع $ \f_1,f_2,\dots,f_N\ $ به پایه ای برای $F$ باشد. لذا $ e_i=\sum_j=1^n \lambda_i j\mathfrak e_j $ برای $ ۰\leqslant i\leqslant N $ و \beginalign* ۰=\sum^N_i=1e_i\otimes f_i=\sum^N_i=1(\sum_j=1^n\lambda_i j\mathfrak e_j)\otimes f_i=\sum_i=1,j=1^N,n\lambda_i j(\mathfrak e_j\otimes f_i) \endalign* چون $\\mathfrak e_\,l\otimesf_k\_L\times K $ پایه ای برای $ E\odot F $ می باشد. لذا $ \lambda_i j=0 $ برای هر $ ۱\leqslant i\leqslant N , 1\leqslant j\leqslant n $ و در نتیجه $ e_1=e_2=\cdots=e_N $ و قسمت اول گزاره اثبات می شود. حال اگر $ \f_k\_K $ پایه ای برای $F$ باشد، پایه ای مانند $ \e_l\_L $ برای $E$ انتخاب می کنیم و در نتیجه هر عضو $E\odot F$ را می توان به صورت یکتا به صورت $\sum \lambda_l k(e_l\otimes f_k)$ نوشت که تعداد متناهی از $\lambda_l k$ غیر صفر می باشند. فرض کنیم $\sum_i=1^n\lambda_i(e_i\otimes f_i)$ عضوی از $E\odot F$ باشد این شکل نمایش همانگونه که گفته شد یکتا می باشد و در نتیجه $\sum_i=1^n\lambda_i(e_i\otimes f_i)=\sum_i=1^n(\lambda_ie_i)\otimes f_i $ و لذا حکم دوم نیز ثابت می شود. $\blacksquare$

#آنالیز #آنالیز_حقیقی #تانسور #ریاضیات #ضرب_تانسوری #فضای_برداری

[mthmtc]

حاصل ضرب تانسوری (۱-فضاهای برداری)

پست جدید انتشار یافت https://mthmtcs.ir/tensor-product-1/

حاصل ضرب تانسوری (۱-فضاهای برداری)

گزاره ۱٫۱ : فرض کنید $G_1,F,E$ و $G_2$ فضاهای برداری و \beginalign* \pi_2 : E \times F \To G_2 \quad , \quad \pi_1 : E \times F \To G_1 \endalign* نگاشتهای دوخطی باشند.اگر برای هر فضای برداری $M$ وهر نگاشت دوخطی $ \chi : E \times F \To M $ نگاشتهای خطی منحصر به فرد \beginalign* \eta_2 : G_2 \To M \qquad , \qquad \eta_1 : G_1 \To M \endalign* وجود داشته باشد بطوریکه $ \eta_2 \! \circ \pi_2 =\chi $ و $ \eta_1 \! \circ \pi_1 =\chi $، آنگاه یک ایزومرفیسم مانند $ \varphi : G_1 \To G_2 $ وجود دارد بطوریکه $ \varphi \circ \pi_1 = \pi_2 $ .

اثبات: ابتدا فرض کنیم $ M = G_2 $ و $ \chi = \pi_2 $ آنگاه بنابر فرض $ \psi_1 : G_1 \To M = G_2 $ بطوریکه $ \psi_1 \circ \pi_1 = \pi_2 $. حال $ M = G_1 $   و $ \chi = \pi_1 $ آنگاه بنابر فرض $ \psi_2 : G_2 \To M = G_1 $ بطوریکه $ \psi_2 \circ \pi_2 = \pi_1 $.  با ترکیب دو رابطه بالا داریم \beginalign* (\psi_1 \circ \psi_2) \circ \pi_1 = \pi_2 \qquad , \qquad (\psi_2 \circ \psi_1) \circ \pi_1 = \pi_1 \endalign* حال چون $ \rm id_G_1 \circ \pi_1 = \pi_1 $ و $ \rm id_G_2 \circ \pi_2 = \pi_2 $ تجزیه های دیگری از این نوع می باشند. لذا بنابر یکتایی تجزیه داریم: \beginalign* \psi_1 \circ \psi_2 = \rm id_G_2 \qquad , \qquad \psi_2 \circ \psi_1 = \rm id_G_1 \endalign* و در نتیجه $ \psi_1 $ یک به یک و پو شا می باشد و $ \psi_1 \circ \pi_1 = \pi_2 $ . در نتیجه $ \varphi = \psi_1 $ و اثبات کامل می شود. $\blacksquare$

نکته ۱٫۱ : با توجه به اثبات گزاره ۱٫۱ شرط یکتایی تجزیه اساسی می باشد. با این حال هنگامی که نگاشتهای $\pi_1$ و $\pi_2$ پوشا هستند و یا بردشان به ترتیب $ G_1 $ و $ G_2 $ را تولید می کند تجزیه یکتاست. فرض کنیم $ \chi : E\times F \To M $ نگاشت دوخطی باشد و $ \beta : G_1 \To M $ و $ \beta’ : G_1 \To M $ دو تجزیه مختلف برای $ \chi $ باشند یعنی $ \beta \circ \pi_1 = \chi $ و $ \beta’ \circ \pi_1 = \chi $. اگر هر $ g \in G_1 $ را بتوان به صورت $ g= \sum \pi_1 (e_i,f_i) $ آنگاه $ \chi =\beta \circ \pi_1 =\beta’ \circ \pi_1 $ نتیجه می دهد که \beginalign* \beta (g) &= \beta \left( \sum \pi_1 (e_i,f_i) \right) = \sum \chi(e_i,f_i)\cr &= \sum \beta'(\pi_1 (e_i,f_i)) = \beta’ \left( \sum \pi_1(e_i,f_i) \right) = \beta'(g) \endalign* لذا  $ \beta = \beta’ $.

ساختار ضرب تانسوری جبری

فرض کنیم $E$ و $F$ فضای برداری باشند

  در حالت کلی $X^(Y)$ مجموعه تمام نگاشتهای از $Y$ بتوی $X$ می باشند بطوریکه دارای برد متناهی هستند. اعمال روی $\Bbb C^(E \times F)$ را به صورت زیر تعریف می کنیم : \beginalign* \sum\lambda(e,f)+\sum\mu(e,f)=\sum(\lambda+\mu)(e,f) \endalign* \beginalign* \mu\sum\lambda(e,f)=\sum(\mu\lambda)(e,f) \endalign* بااین اعمال $\Bbb C^(E \times F)$ به فضای برداری روی $\Bbb C$ با پایهٔ $E\times F$ تبدیل می شود. حال زیر فضای برداری تولید شده توسط عناصر زیر را $ \calN $ می نامیم \beginalign* (e_1+e_2,f)-(e_1,f)-(e_2,f) \endalign* \beginalign* (e,f_1+f_2)-(e,f_1)-(e,f_2) \endalign* \beginalign* \lambda(e,f)-(\lambda e,f)\quad \mboxو\quad \lambda(e,f)-(e,\lambda f) \endalign* که $ e,e_1,e_2 \in E ,\ f,f_1,f_2 \in F $ و $ \lambda \in \Bbb C $ . حال ضرب تانسوری جبری $E$ و $F$ را فضای خارج قسمتی \beginalign*E \odot F := \Bbb C^(E \times F)/ \cal N \endalign* تعریف می کنیم. حال اگر $\pi$ نگاشت خارج قسمتی از $\Bbb C^(E\times F)$ بروی $E\odot F$ باشد آنگاه چون \beginalign* \lambda(e,f)-(\lambda e,f)\in\cal N\quad \mboxو\quad (e_1+e_2,f)-(e_1,f)-(e_2,f)\in\cal N \endalign* \beginalign* \lambda(e,f)-(e,\lambda f)\in\cal N\quad \mboxو\quad (e,f_1+f_2)-(e,f_1)-(e,f_2)\in\cal N \endalign* داریم \beginalign* \pi(\lambda e_1+e_2,f)=\lambda\pi(e_1,f)+\pi(e_1,f) \endalign* \beginalign* \pi(e,\lambda f_1+f_2)=\lambda\pi(e,f_1)+\pi(e,f_2) \endalign* لذا تحدید $\pi$ بروی $E\times F$ دوخطی می باشد. عناصر $\pi(e,f)\in E\odot F$ که $e\in E,\ f\in F$ را عناصر ابتدایی می نامیم و با $e\otimes f$ نمایش می دهیم. چون $\pi$ پوشا می باشد هر عضو $t$ در $E\odot F$ را می توان به صورت مجموع متناهی از عناصر ابتدایی نوشت. \beginalign* t= \sum_i=1^N e_i\otimes f_i \endalign* اما این مجموع یکتا نیست چون $\pi$ یک به یک نیست. با توجه به ساختار $E\odot F$ داریم \beginalign* (e_1+e_2)\otimes f=e_1\otimes f+e_2\otimes f \endalign* \beginalign* e\otimes(f_1+f_2)=e\otimes f_1+e\otimes f_2 \endalign* \beginalign* \lambda(e\otimes f)=\lambda e\otimes f=e\otimes \lambda f \endalign* از روابط بالا آشکار است که برای هر $e\in E,\ f\in F$ داریم \beginalign* ۰=۰\otimes 0=0\otimes f=e\otimes 0 \endalign*

گزاره ۲٫۱ : فرض کنید $F,E$ فضای برداری و $\pi:E\times F\To E\odot F$ نگاشت دوخطی کانونی باشد.اگر $M$ یک فضای برداری و $\psi:E\times F\To M$ نگاشت دوخطی باشد آنگاه $\psi$ بطوریکتا روی $E\odot F$ توسیع می یابد یعنی نگاشت خطی یکتای $\varphi:E\odot F\To M$ وجود دارد بطوریکه $\varphi\circ\pi=\psi$.

اثبات: ابتدا $\psi$ را با استفاده از خاصیت خطی به نگاشت خطی $\tilde\psi :\mathbb C^(E\times F)\To M$ بصورت زیر توسیع می دهیم \beginalign*\tilde\psi \left(\sum\lambda(e,f)\right)=\sum\lambda\psi(e,f),\qquad e\in E,\ f\in F,\ \lambda\in\mathbb C \endalign* با توجه به خواص خطی $ \psi $ واضح است که $ \tilde\psi(\mathcal N)=0 $. حال نگاشت $ \varphi:E\odot F\To M $ را به صورت زیر تعریف می کنیم. فرض کنیم $ t\in E\odot F $ پس $ x\in \mathbb C^(E\times F) $ وجود دارد بطوریکه $ \pi(x)=t $ قرار می دهیم $ \varphi(t)=\tilde\psi(x)$. حال چون $ \tilde\psi(\mathcal N)=0 $ ، اگر $ t_1 , t_2 \in E\odot F $ و $ t_1=t_2 $ لذا $ t_1-t_2\in\mathcal N $ و در نتیجه $ \tilde\psi(t_1-t_2)=0 $ و $ \varphi(t_1)=\varphi(t_2) $ . لذا $ \varphi $ خوشتعریف است. فرض کنیم $ \gamma\in\mathbb C\ ,\ t_1=\pi(\sum\lambda(e,f))\in E\odot F\ ,\ t_2=\pi(\sum\mu(e,f))\in E\odot F $ پس \beginalign* \varphi(\gamma t_1+t_2)&=\varphi(\gamma(\pi(\sum\lambda(e,f)))+\pi(\sum\mu(e,f)))\\ &=\varphi(\pi(\sum(\gamma\lambda+\mu)(e,f))= \tilde\psi(\sum(\gamma\lambda+\mu)(e,f))\\ &=\tilde\psi(\sum(\gamma\lambda(e,f))+ \tilde\psi(\sum\mu(e,f))= \gamma(\tilde\psi(\sum\lambda(e,f)))+\tilde\psi(\sum\mu(e,f))\\ &=\gamma(\varphi(\pi(\sum\lambda(e,f))))+ \varphi(\pi(\sum\mu(e,f)))\\ &=\gamma(\varphi(t_1))+\varphi(t_2) \endalign* لذا $ \varphi $ خطی می باشد و داریم $ \varphi\circ\pi(e,f)=\psi(e,f)$. $\blacksquare$

نکته ۲٫۱ : بنابر گزاره بالا می توان گفت $E\odot F$ فضای برداری یکتای است بطوریکه برای هر فضای برداری $ M $ داریم \beginalign* \rm\bf Bil(E\times F ,\ M)\simeq\rm\bf Lin(E\odot F ,\ M) \endalign* توجه داریم که پیوستگی $ \psi $ پیوستگی $ \varphi $ را ایجاب نمی کند حتی اگر $ \pi $ پیوسته باشد. ما این مطلب را بعداً مورد بررسی قرار می دهیم.

گزاره ۳٫۱ : اگر $ \ e_j \_\mathcal J $ پایه‌ای برای $ E $ و $ \ f_k \_\mathcal K $ پایه‌ای برای $ F $ باشد. آنگاه $ \e_j\otimes f_k\_\mathcal J\times\mathcal K $ پایه‌ای برای $ E\odot F $ می باشد و $ \rm dim(E\odot F)=\rm dim(E)\rm dim(F) $ . علاوه بر این داریم \beginalign* E^(\mathcal K)\simeq E\odot F\simeq F\odot E \quad\mboxو\quad E\odot(F\odot G)\simeq(E\odot F)\odot G \endalign* که $ E^(\mathcal K) $ فضای تمامی نگاشتها از $\mathcal K $ بتوی $ E $ با برد متناهی می باشند.

اثبات: فرض کنیم $ G_1:=E\odot F $ و $ G_2:=E^(\mathcal K) $ . گزاره ۱٫۱ را بکار می بریم و ثابت می کنیم که $ G_1\simeq G_2 $ . نگاشتهای دوخطی $ \pi_1:E\times F\To G_1 $ و $ \pi_2:E\times F\To G_2 $ بصورت زیر تعریف می کنیم \beginalign* \pi_1:(e,f)\mapsto e\otimes f\ ,\quad \pi_2:(e,\sum_k\in\mathcal K\lambda_kf_k )\mapsto(\lambda_ke)_k\in\mathcal K \endalign* توجه داریم که $ G_1 $ و $ G_2 $ توسط برد نگاشتهای $ \pi_1 $ و $ \pi_2 $ تولید می شود. مجموعهٔ \beginalign* \\ \pi_2(e_j,f_k)=(\delta_k i\,e_j)_i\in\mathcal K\ ;\ (j,k)\in \mathcal J\times K\ \ \endalign* پایه‌ای برای $ E^(\mathcal K) $ می باشد. فرض کنید $ \chi $ نگاشتی دو خطی از $ E\times F $ به توی فضای برداری $ M $ باشد. با استفاده از گزاره ۲٫۱ نگاشت خطی منحصر بفرد $ \eta_1:E\odot F\To M $ بطوریکه $ \eta_1\circ\pi_1=\chi $. حال نگاشت $ \eta_2:E^(\mathcal K)\To M $ را به صورت زیر تعریف می کنیم \beginalign* \eta_2((e_k)_\mathcal K):=\sum_\mathcal K \chi(e_k,f_k) \endalign* چون $ \chi $ دوخطی می باشد لذا $ \eta_2 $ خطی می باشد و داریم \beginalign* \eta_2\circ\pi_2(e,\sum_\mathcal K\lambda_kf_k)=\eta_2((\lambda_ke)_\mathcal K)=\sum_\mathcal K\chi(\lambda_ke,f_k)=\chi(e,\sum_\mathcal K\lambda_kf_k) \endalign* پس $ \eta_2\circ\pi_2=\chi $. و با استفاده از گزاره ۱٫۱ نتیجه می شود که $ E\odot F\simeq E^(\mathcal K) $ و یک ایزومرفیسم $ \varphi:E\odot F\To E^(\mathcal K) $ بطوریکه $ \varphi\circ\pi_1=\pi_2 $. بویژه $ \varphi(e_j\otimes f_k)=\pi_2(e_j,f_k) $ و در نتیجه مجموعهٔ \beginalign* \ e_j \otimes f_k\ ;\ (e_j,f_k)\in\mathcal J\times K \=\varphi^-1 \ \pi_2 (e_j,f_k)\ ;\ (j,k)\in\mathcal J\times K \ \endalign* که تصویر ایزومرفیک پایه‌ای از $ E^(\mathcal K) $ می باشد، پایه‌ای برای $ E\odot F $ می باشد. حال نگاشت خطی القا شده توسط نگاشت دوخطی $ (e,f)\mapsto f\otimes e $ را در نظر می گیریم واضح است که $ \phi $ ایزومرفیسم می باشد چون پایه را به پایه می برد و لذا $ E\odot F\simeq F\odot E $. بطور مشابه نگاشت $ \phi:(e,f\otimes g)\mapsto (e\otimes f)\otimes g $ از $ E\times(F\odot G) $ بتوی $ (E\odot F)\odot G $ دوخطی می باشد زیرا \beginalign* \phi((\lambda e_1+e_2),f\otimes g)&=((\lambda e_1+e_2)\otimes f)\otimes g\cr &=(\lambda(e_1\otimes f))\otimes g+(e_2\otimes f)\otimes g\cr &=\lambda\phi((e_1,f\otimes G))+\phi((e_2,f\otimes G)) \endalign* \beginalign* \phi(e,\lambda(f_1\otimes g_1)+f_2\otimes g_2)=\lambda\phi(e,f_1\otimes g_1)+\phi(e,f_2\otimes g_2) \endalign* حال نگاشت القا شده توسط $ \phi $ درنظر می گیریم که یک ایزومرفیسم از $ E\odot (F\odot G) $ به $ (E\odot F)\odot G $ می باشد. $\blacksquare$

از گزاره بالا داریم $ E\odot F $ و $ F\odot E $ بطورجبری ایزومرفیسم می باشند اما نرمهای نامتقارنی وجود دارند که $ E\odot F $ و $ F\odot E $ را تبدیل به فضاهای نرمدار متفاوتی می کند.

گزاره ۴٫۱ : فرض کنیم $ f_1,f_2,\dots,f_N\in F $ مستقل خطی باشند. اگر $ e_1,e_2,\dots,e_N\in E $ و $ \sum_i=1^Ne_i\otimes f_i=0$ آنگاه $ e_1=e_2=\cdots=e_N=0 $. بویژه اگر $ \f_k\_K $ پایه ای برای $F$ باشد آنگاه هر $ t\in E\odot F $ نمایش منحصر به فرد $ \sum_Ne_k\otimes f_k $ (مجموع متناهی) دارد.

اثبات: فرض کنیم $ \ \mathfrak e_1,\mathfrak e_2,\dots,\mathfrak e_n \ $ پایه ای برای $ \mathfrak E :=\rm Span\e_1,e_2,\dots,e_N\ $ واضح است که $ n\leqslant N $ و $ \\mathfrak e_\,l\_L $ توسیع $ \\mathfrake_1,e_2,\dots,e_n\ $ به پایه ای برای $ E $ باشد و $ \f_k\_K $ توسیع $ \f_1,f_2,\dots,f_N\ $ به پایه ای برای $F$ باشد. لذا $ e_i=\sum_j=1^n \lambda_i j\mathfrak e_j $ برای $ ۰\leqslant i\leqslant N $ و \beginalign* ۰=\sum^N_i=1e_i\otimes f_i=\sum^N_i=1(\sum_j=1^n\lambda_i j\mathfrak e_j)\otimes f_i=\sum_i=1,j=1^N,n\lambda_i j(\mathfrak e_j\otimes f_i) \endalign* چون $\\mathfrak e_\,l\otimesf_k\_L\times K $ پایه ای برای $ E\odot F $ می باشد. لذا $ \lambda_i j=0 $ برای هر $ ۱\leqslant i\leqslant N , 1\leqslant j\leqslant n $ و در نتیجه $ e_1=e_2=\cdots=e_N $ و قسمت اول گزاره اثبات می شود. حال اگر $ \f_k\_K $ پایه ای برای $F$ باشد، پایه ای مانند $ \e_l\_L $ برای $E$ انتخاب می کنیم و در نتیجه هر عضو $E\odot F$ را می توان به صورت یکتا به صورت $\sum \lambda_l k(e_l\otimes f_k)$ نوشت که تعداد متناهی از $\lambda_l k$ غیر صفر می باشند. فرض کنیم $\sum_i=1^n\lambda_i(e_i\otimes f_i)$ عضوی از $E\odot F$ باشد این شکل نمایش همانگونه که گفته شد یکتا می باشد و در نتیجه $\sum_i=1^n\lambda_i(e_i\otimes f_i)=\sum_i=1^n(\lambda_ie_i)\otimes f_i $ و لذا حکم دوم نیز ثابت می شود. $\blacksquare$

#آنالیز #آنالیز_حقیقی #تانسور #ریاضیات #ضرب_تانسوری #فضای_برداری

[mthmtc]

حاصل ضرب تانسوری (۳- نرم روی ضرب تانسوری جبری)

پست جدید انتشار یافت https://mthmtcs.ir/tensor-product-3/

حاصل ضرب تانسوری (۳- نرم روی ضرب تانسوری جبری)

تا بحال ساختار جبری ضرب تانسوری دو فضای برداری را بررسی کردیم، حال با تعریف یک نرم روی این ضرب تانسوری پوستگی نگاشتها را روی کامل شده این فضا بوسیله این نرم را بررسی می کنیم. فرض کنیم $\alpha$ یک نرم روی $A\odot B$ ، ضرب تانسوری جبرهای $A$ و $B$ باشد کامل شده $A\odot B$ تحت این نرم با $A\otimes_\alphaB$ نمایش می دهیم. ما علاقه مندیم نرمهای را بررسی کنیم که با استفاده از نرمهای موجود روی $A$ و $B$ ساخته می شوند.

گزاره ۶٫۱ : فرض کنیم $A$ و $B$ فضاهای برداری باشند و $\cal A\subseteq A$ و $\cal B\subseteq B$ زیر فضا باشند، آنگاه $\cal A\odot B$ در $A\odot B$ نشانده می شود. بویژه اگر $\alpha$ یک نرم روی $A\odot B$ و $\hat\alpha$ تحدید $\alpha$ بروی $\cal A\odot B$ باشد، آنگاه $\cal A\otimes_\hat\alpha\cal B\subseteq A\otimes_\alpha B$.

اثبات: فرض کنیم نگاشت خطی $\imath:\cal A\odot\cal B\To A\odot B$ توسیع نگاشت دوخطی $(e,f)\mapsto e\otimes f$ باشد. ثابت می کنیم که $\imath$ یک به یک می باشد. فرض کنیم $t\in\cal A\odot\cal B$ بطوریکه $\imath(t)=t=0$. حال اگر $\f_i\$ پایه‌ای برای $\cal B$ باشد پس $t$ بطوریکتا بصورت $\sum e_i\otimes f_i$ نوشته می شود. لذا $\imath(\sum e_i\otimes f_i)=\sum e_i\otimes f_i=0$. حال چون $\f_i\$ در $B$ مستقل خطی می باشد، پس $e_i=0$ برای هر $i$. لذا $t=0$ در $\cal A\odot B$ و $\imath$ یک به یک می باشد. حال با توجه به اینکه $\cal A\odot B$، $\alpha$-نرم زیرفضای $A\otimes_\alphaB$ می باشد. لذا کامل شده آن نیز زیر فضای $A\otimes_\alphaB$ می باشد. $\blacksquare$

تعریف ۱٫۱ : فرض کنیم $B,A$ فضاهای نرم دار باشند. نرم $\alpha$ روی $A\odot B$ را نرم زیرکراس ((subcross norm))نامیم، اگر برای هر $a\in A\,,\ b\in B$ داشته باشیم $\alpha(a\otimes b)\leq \|a\|\|b\|$. و نرم کراس ((cross norm))نامیم، اگر برای هر $a\in A\,,\ b\in B$ داشته باشیم $\alpha(a\otimes b) = \|a\|\|b\|$.

لم ۱٫۱ : فرض کنیم $B,A$ جبر و $(u_\nu)_N, (\upsilon_\mu)_M$ بترتیب تقریب کراندار ((یک تقریب واحد کراندار در جبر نرمدار $A$، تور $\u_i\$ از عناصر $A$ می باشد بطوریکه $\|u_ix-x\|\rightarrow 0$ و $\|xu_i-x\|\rightarrow 0$ برای هر $x\in A$)) واحدهای $B,A$ باشد. اگر $\alpha$ نرم زیرکراس روی $A\odot B$ باشد آنگاه $(u_\nu\otimes\upsilon_\mu)_N\times M$ یک تقریب واحد بر حسب $\alpha$روی $A\odot B$.

اثبات: برای هر $\sum a_i\otimes b_i\in A\odot B$ داریم \begineqnarray* \alpha\left[(\sum a_i\otimes b_i)(u_\nu\otimes\upsilon_\mu)-\sum a_i\otimes b_i\right] &=&\alpha(\sum a_iu_\nu\otimes b_i\upsilon_\mu-a_i\otimes b_i)\\ &\leq&\sum\alpha(a_iu_\nu\otimes b_i\upsilon_\mu-a_i\otimes b_i)\\ &\leq&\sum\alpha(a_iu_\nu\otimes b_i\upsilon_\mu-a_iu_\nu\otimes b_i+a_iu_\nu\otimes b_i-a_i\otimes b_i)\\ &\leq&\sum\alpha(a_iu_\nu\otimes(b_i\upsilon_\mu-b_i)-(a_i-a_iu_\nu\otimes b_i)\\ &\leq&\|a_iu_\nu\|\|b_i\upsilon_\mu-b_i\|+\|a_i-a_iu_\nu\|\|b_i\|\rightarrow 0 \endeqnarray* لذا $(u_\nu\otimes\upsilon_\mu)_N\times M$ یک تقریب واحد بر حسب $\alpha$ می باشد. $\blacksquare$

لم ۲٫۱ : فرض کنید $A$ $B$ جبرهای نرمدار و $A^*$ و $B^*$ بترتیب دوگان این جبرها باشند. آنگاه مجموعه $\\ f_A\odot f_B\ ;\ f_A\in A^*\ ,\ f_B\in B^*\ \$ نقاط $A\odot B$ را جدا می کند.

اثبات: فرض کنیم $t=\sum a_i\otimes b_i\in A\odot B\backslash \0\$ و $b_i$ ها مستقل خطی و $a_1\neq 0$ باشند. بنا بر قضیه هان باناخ $f_A\in A^*$ و $f_B\in B^*$ وجود دارد بطوریکه \beginalign* f_A(a_1)=\|a_1\|\quad ,\quad 0\neq s=f_B(b_1)\quad , \quad f_B(\rm Span\b_2,\dots,b_n\)=0 \endalign* لذا $(f_A\odot f_B)(t)=\sum f_A(a_i)f_B(b_i)=f_A(a_1)f_B(b_1)\neq 0$. $\blacksquare$

تعریف : فرض کنید $A,B$ فضاهای نرمدار باشند و $t\in A\odot B$. توابع $\gamma$ و $\lambda$ را بصورت زیر تعریف می کنیم: \beginalign* \gamma(t):=\inf\left\\ \endalign* \beginalign* \lambda(t):=\sup\left\\leq 1\right\ \endalign*

گزاره ۷٫۱ : توابع $\gamma$ و $\lambda$ نرم کراس هستند و $\gamma$ بزرگترین شبه نرم زیرکراس روی $A\odot B$ می باشد. هنگامی که $A$ و $B$ جبر می باشند، $\gamma$ زیر ضربی می باشد و $A\otimes_\gammaB$ جبر باناخ می باشد.

اثبات: ابتدا ثابت می کنیم که $\lambda$ یک نرم کراس می باشد. فرض کنیم $t\in A\odot B$ پس $t=\sum a_i\otimes b_i$ و برای هر $f_B\in B^*,f_A\in A^*$ که $\|f_A\|,\|f_B\|\leq1$ داریم \beginalign* \|(f_A\odot f_B)(\sum a_i\otimes b_i)\|&=\|\sum f_A(a_i)f_B(b_i)\|\cr &\leq\sum\|f_A(a_i)\|\|f_B(b_i)\|\cr &\leq\sum\|a_i\|\|b_i\| \endalign* و چون $t$ همواره بصورت مجموع متناهی از تانسورهای ابتدایی می باشد لذا $\lambda(t)$ متناهی می باشد. از طرفی نامساوی مثلثی نیز به وضوح برقرار می باشد زیرا \beginalign* \|(f_A\odot f_B)(\sum a_i\otimes b_i+\sum a_i^\prime\otimes b_i^\prime)\| \leq\|(f_A\odot f_B)(\sum a_i\otimes b_i)\|+\|(f_A\odot f_B)(\sum a_i^\prime\otimes b_i^\prime)\| \endalign* و اگر $\mu\in \Bbb C$ و $t=\sum a_i\otimes b_i\in A\odot B$ پس داریم \beginalign* \lambda(\mu t)=|\mu|\lambda(t) \endalign* زیرا $\|(f_A\odot f_B)(\mu t)\|=|\mu|\|(f_A\odot f_B)(t)\|$. حال اگر $\lambda(t)=0$ آنگاه با استفاده از گزاره ۲٫۱ نتیجه می شود که $t=0$. لذا $\lambda$ نرم می باشد. $\lambda$ کراس نرم نیز می باشد زیرا \beginalign* \lambda(a\otimes b)=\sup\\=\sup\\\leq\|a\|\|b\| \endalign* چون سوپریمم روی تمام فانکشنالهای با نرم حداکثر ۱ می باشد لذا بنا بر قضیه هان باناخ فانکشنالهای $g_A,g_B$ وجود دارد بطوریکه $g_A(a)=\|a\|$ و $g_B(b)=\|b\|$و در نتیجه $\lambda(a\otimes b)=\|a\|\|b\|$ . واضح است که $\gamma$ یک تابع حقیقی می باشد و برای هر $t,t_1,t_2\in A\odot B$ و $\mu\in\Bbb C$، با استفاده از خواص سوپریمم داریم: \beginalign* \gamma(t_1+t_2)\leq\gamma(t_1)+\gamma(t_2)\qquad,\qquad \gamma(\mu t)=|\mu|\gamma(t) \endalign* لذا $\gamma$ یک شبه نرم و زیر کراس می باشد. حال ثابت می کنیم که $\gamma$ یک نرم می باشد. اگر $\alpha$ یک شبه نرم زیر کراس روی $A\odot B$ باشد، آنگاه $\alpha(\sum a_i\otimes b_i)\leq\sum\alpha(a_i\otimes b_i)\leq\sum\|a_i\|\|b_i\|$. لذا $\alpha(t)\leq\gamma(t)$ برای هر $t\in A\odot B$. فرض کنیم $(t\neq0)\in A\odot B$ لذا چون $\gamma$ یک زیر کراس می باشد، پس داریم $۰ $\blacksquare$

گزاره ۸٫۱ :

فرض کنید $B_1,B_2$ و $A_1,A_2$ فضاهای برداری و $\psi_1:A_1\To B_1$ و $\psi_2:A_2\To B_2$ نگاشتهای خطی کراندار باشد. آنگاه نگاشت $\psi_1\odot\psi_2:A_1\odot A_2\To B_1\odot B_2$ بطور پیوسته به نگاشتهای خطی پیوسته $\psi_1\otimes_\gamma\psi_2:A_1\otimes_\gamma A_2\To B_1\otimes_\gamma B_2$ و $\psi_1\otimes_\lambda\psi_2:A_1\otimes_\lambdaA_2\To B_1\otimes_\lambdaB_2$ توسعه می یابد.

اگر $f_1\in A^*_1,f_2\in A^*_2$ آنگاه $\|(f_1\odot f_2)(t)\|\leq\|f_1\|\ \|f_2\|\lambda(t)$. بویژه فانکشنال $f_1\odot f_2:A_1\odot A_2\To \Bbb C$ با هر دو نرم $\gamma$ و $\lambda$ پیوسته می باشد.

اگر $C$ یک جبر و $\varphi_1:A_1\To C$ و $\varphi_2:A_2\To C$ نگاشتهای خطی کرانداری باشند که با هم جابجا می شوند، آنگاه $\varphi_1\odot\varphi_2:A_1\odot A_2\To C$ نسبت به نرم $\gamma$ پیوسته می باشد.

اثبات: ابتدا (۲) را ثابت می کنیم. بوسیله تعریف $\gamma$ داریم: \beginalign* \|(f_1\odot f_2)(\sum a_1,i\otimes a_2,i)&=\|\sum f_1(a_1,i)f_2(a_2,i)\|\cr &=\|f_1\|\ \|f_2\|\ \|\sum\fracf_1(a_1,i)\fracf_2\(a_2,i)\|\cr &\leq\|f_1\|\ \|f_2\|\lambda(\sum a_1,i\otimes a_2,i) \endalign* لذا $f_1\odot f_2$ نسبت به $\lambda$ و $\gamma$ پیوسته می باشد.($\lambda\leq\gamma$) حال (۳) را اثبات می کنیم \beginalign* \|(\varphi_1\odot\varphi_2)(\sum a_1,i\otimes a_2,i)\|&=\|\sum\varphi_1(a_1,i)\varphi(a_2,i)\|\cr &\leq\|\varphi_1\|\ \|\varphi_2\|\sum\|a_1,i\|\ \|a_2,i\| \endalign* با اینفیمم گیری از طرف راست داریم \beginalign* \|(\varphi_1\odot\varphi_2)(\sum a_1,i\otimes a_2,i)\|\leq\|\varphi_1\|\ \|\varphi_2 \gamma(\sum a_1,i\otimes a_2,i) \endalign* لذا $\varphi_1\odot\varphi_2$ نسبت به نرم $\gamma$ پیوسته می باشد. و در آخر (۱) را ثابت می کنیم \beginalign* \gamma((\psi_1\odot\psi_2)(\sum a_1,i\otimes a_2,i))=\gamma(\sum\psi_1(a_1,i)\otimes\psi_2(a_2,i))\leq \|\psi_1\|\ \|\psi_2\|\sum\|a_1,i\|\ \|a_2,i\| \endalign* و در نتیجه $\gamma(\psi_1\odot\psi_2)(t)\leq\|\psi_1\|\ \|\psi_2\|\gamma(t)$ . و درنهایت ثابت می کنیم که $\psi_1\odot\psi_2$ نسبت به نرمهای $\lambda$ نیز پیوسته می باشد. فرض کنیم $g_1\in B_1^*$ و $g_2\in B_2^*$و $\|g_1\|,\|g_2\|\leq1$ آنگاه $g_1\circ\psi_1\in A_1^*$ و $g_2\circ\psi_2\in A_2^*$ و $\|g_1\circ\psi_1\|\leq\|\psi_1\|$ و $\|g_2\circ\psi_2\|\leq\|\psi_2\|$ و داریم \beginalign* (g_1\circ\psi_1)\odot(g_2\circ\psi_2)=(g_1\odot g_2)\circ(\psi_1\odot\psi_2) \endalign* \begineqnarray* \lambda(\psi_1\odot\psi_2(t))&=&\sup_g_1,g_2\\ \\\ &=&\sup_g_1,g_2\\ \\\ &\leq&\|\psi_1\|\ \|\psi_2\|\ \lambda(t) \endeqnarray* و در نتیجه $\psi_1\odot\psi_2$ پیوسته می باشد. $\blacksquare$

گزاره ۹٫۱ : فرض کنید $C,B,A$ جبر و $\alpha$ یک نرم جبر زیرکراس و $B,A$ یکدار باشند. برای هر نگاشت خطی ضربی پیوسته مانند $\xi:A\otimes_\alphaB\To C$، نگاشتهای خطی ضربی پیوسته که با هم جابجا می شوند مانند $\varphi:A\To C$ و $\psi:B\To C$ وجود دارد بطوریکه $\varphi\odot\psi:A\odot B\To C$، $\alpha$-پیوسته می باشد و $\xi=\varphi\otimes_\alpha\psi$ .

اثبات: فرض کنیم $\varphi(a):=\xi(a\otimes 1)$ و $\psi(b):=\xi(1\otimes b)$. آنگاه $\varphi:A\To C$ و $\psi:B\To C$ خطی و چون $\alpha$ زیرکراس می باشد پیوسته می باشند. علاوه بر این چون \beginalign* \varphi(a)\psi(b)=\xi((a\otimes1)(1\otimes b))=\xi(a\otimes b)=\xi((1\otimes b)(a\otimes1))= \psi(1\otimes b)\varphi(a\otimes1) \endalign* لذا $\varphi\odot\psi:A\odot B\To C$ تعریف شده و $(\varphi\odot\psi)(t)=\xi(t)$ برای هر $t\in A\odot B$. بویژه $\varphi\odot\psi$، $\alpha$-پیوستگی را از $\xi$ به ارث می برد و در نتیجه $\varphi\otimes_\alpha\psi=\xi$. $\blacksquare$

تعریف ۳٫۱ : فرض کنیم $\alpha$ یک نرم روی $A\odot B$ باشد. تابع $\alpha^*:A^*\odot B^*\To [0,\infty]$ تعریف شده بصورت

\beginalign* \alpha^*(f)\ :=\ \sup\\ ;\ x\in A\odot B\ ,\ \alpha(x)\le1\ \,\quad f\in A^*\odot B^* \endalign* را نرم دوگان ((dual norm )) $\alpha$ خوانیم.

گزاره ۱۰٫۱ :

اگر $\alpha^*$ متناهی باشد، آنگاه آن یک نرم روی $A^*\odot B^*$ می باشد

اگر $f_A\in A^*$و $f_B\in B^*$ آنگاه \beginalign* \|(f_A\odot f_B)(t)\|\le\alpha^*(f_A\odot f_B)\cdot\alpha(t)\qquad\qquad t\in A\odot B\ \mboxبرای هر \endalign*

$f_A\odot f_B$$\alpha$-پیوسته می باشد اگر و تنها اگر $\alpha^*(f_A\odot f_B)

$\alpha$ نرم زیرکراس می باشد اگر و تنها اگر $\alpha\le\gamma$.

$\alpha^*$ نرم زیرکراس می باشد اگر و نتها اگر $\lambda\le\alpha$.

اگر $\alpha$ و $\alpha^*$ نرم زیرکراس باشند آنگاه $\lambda\le\alpha\le\gamma$.

اگر $\lambda\le\alpha\le\gamma$ آنگاه $\alpha$ و $\alpha^*$ نرمهای کراس هستند.

بویژه $\lambda$ کوچکترین نرم کراس می باشد بطوریکه نرم دوگانش نیز نرم کراس می باشد.

اثبات: فرض کنیم $\alpha^*$ متناهی باشد ثابت می کنیم که $\alpha^*$ نرم می باشد. اگر $f,f_1,f_2\in A^*\odot B^*$ و $\zeta\in\Bbb C$ \beginalign* \alpha^*(\zeta f)&=\ \sup\\ \\cr &=\ |\zeta|\sup\\ ;\ x\in A\odot B\ ,\ \alpha(x)\le1\ \=|\zeta|\alpha^*(f) \endalign* \beginalign* \alpha^*(f_1+f_2)&=\ \sup\(f_1+f_2)(x)\\cr &=\ \sup\f_1(x)+f_2(x)\\cr &\le\ \sup\f_2(x)\\cr &\le\ \sup\\ \+ \sup\f_2(x)\\cr &\le\alpha^*(f_1)+\alpha^*(f_2) \endalign* حال فرض کنیم $\alpha^*(f)=0$ و $f=\sum f_i\otimes g_i$ که $f_i\in A^*$ و $g_i\in B^*$ و $g_i$ ها مستقل خطی هستند. لذا $\sup\f(\fracx\alpha(x))\=0$ و در نتیجه $\|f(\fracx\alpha(x))\|=0$ برای هر $(x\ne0)\in A\odot B$. پس $f(x)=0$ برای هر $x\in A\odot B$. حال اگر $a\in A$ و $b\in B$ داریم \beginalign* (\sum f_i\otimes g_i)(a\otimes b)=\sum f_i(a)g_i(b)=0 \endalign* پس $f_i(a)=0$ برای هر $a\in A$ و در نتیجه $f=\sum f_i\otimes g_i=0$. لذا $\alpha^*$ نرم می باشد و این (۱) را ثابت کرد. برای اثبات (۲) کافی است دقت کنیم که برای هر $(t\ne0)\in A\odot B$ داریم $\|(f_A\odot f_B)(\fract\alpha(t))\|\le\alpha^*(f_A\odot f_B)$ و در نتیجه برای هر $t\in A\odot B$ \beginalign* \|(f_A\odot f_B)(t)\|\le\alpha^*(f_A\odot f_B)\cdot\alpha^*(t) \endalign* اگر $f_A\odot f_B$، $\alpha$-پیوسته باشد، آنگاه عدد مثبت $M$ وجود دارد بطوریکه $\|(f_A\odot f_B)(t)\|\le M\alpha(t)$ و \beginalign* \alpha^*(f_A\odot f_B)=\sup\(f_A\odot f_B)(t)\\le M \endalign* برعکس اگر $\alpha^*(f_A\odot f_B) $\blacksquare$

تعریف ۴٫۱ : نرم $\alpha$روی ضرب تانسوری فضاهای نرمدار را معقول خوانیم اگر $\lambda\le\alpha\le\gamma$. لذا بنابر گزارههای ۱۰٫۱ و ۸٫۱، ضرب تانسوری فانکشنالهای پیوسته نسبت به هر نرم معقول پیوسته می باشد و $\psi_1\odot\psi_2:A_1\odot A_2\To B_1\odot B_2$، $\alpha$-$\lambda$-پیوسته و $\gamma$-$\alpha$-پیوسته می باشد نسبت به هر نرم معقول $\alpha$. در آینده نزدیک نشان خواهیم داد که هر $C^*$-نرم، معقول می باشد.

مثال ۲٫۱ :

اگر $(X,\mu)$ فضای اندازه و $E$ یک فضای باناخ باشد. آنگاه $L^1(X,\mu)\otimes_\gammaE$ با $L^1(X,\mu,E)$، فضای تمام توابع $\mu$-انتگرالپذیر از $X$ بتوی $E$، ایزومرفیک می باشد. این ایزومرفیسم از نگاشت دوخطی $(f,\eta)\mapsto(x\mapsto f(x)\eta)$ که از $L^1(X,\mu)$ بتوی $L^1(X,\mu,E)$ تعریف می شود، ایجاد می شود.

بعنوان مثال دیگر $C^*$-ایزمرفیسم بودن $C_0(X)\otimes_\alphaA$ با $C_0(X\rightarrow A)$ . که $X$ فضای هاسدورف موضعا فشرده و $A$ یک $C^*$-جبر و $\alpha$ یک $C^*$-نرم می باشد.

#tensor #tensor_product #تانسور #ضرب_تانسوری #فضای_برداری #نرم