#doing all this time trying to give him the tools to solve math & geometry problems 😩🤡 | Explore Tumblr Posts and Blogs

thousandmaths · 7 years

Text

The Schubert Problem

This is the first in a little two-part sequence about the history of the Schubert calculus. I like this story a lot because it highlights the really human aspect of doing math, and gives lie to the myth that good mathematics only comes from rigorous logical reasoning. Both of these posts are intended to be roughly independent and nontechnical (with the second one, admittedly, a bit more detail-oriented than the first).

-------

If you study some of the more geometric aspects of math, you at some point start to encounter a lot of objects having the name ‘Schubert’ attached to them: Schubert varieties, Schubert classes, Schubert polynomials. So who was Schubert, anyway?

Hermann Schubert was a German mathematician who worked in the mid-to-late 1800s. Note that he is not Franz Schubert, the famous Classical composer; instead he was a high-school teacher. Although not a member of the university system, he was an active researcher, working in a particularly combinatorial corner of algebraic geometry.

The trouble started when Schubert was trying to answer questions like the following:

Fix four lines in three-dimensional space, no two of which are parallel or intersecting. How many lines intersect all four of them?

If you’re anything like me, you say: there’s no way that’s enough information to give an answer, or even if it is, there’s no way the answer is anything interesting. But in fact, a miracle occurs. Not only is there an answer, but the answer is always the same: there are exactly two such lines!

Schubert was part of a group of people who were interested in answering these questions, and he figured out a brilliant way to do it. You could presumably figure this out by some very long and arduous computations with coordinates, but that’s not what Schubert did. For instance, this is how Schubert solved the problem above:

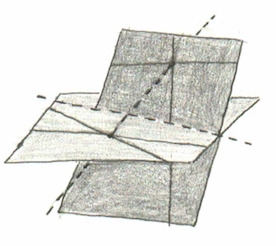
Let’s solve an easier problem: suppose that there are two pairs of intersecting lines in three-dimensional space, no two of which are parallel. Now, there is one obvious line that meets all four of the others: passing between the two points of intersection. A second line can be constructed as follows: each pair of intersecting lines spans a plane, so take the two planes defined by each pair, and they intersect in a line: that line meets all four of the others.

Now, pick one of the pairs of lines, and pull them apart (slowly?). By continuity considerations, there will still be two lines that intersect all four of them. And then do the same for the other pair and of course there will still be two lines that intersect all four, by conservation of number.

The first time you see this, you may not find this argument very convincing.

Well, turns out nobody else did either.

They said “now, wait just a second here, Schubes. What are these continuity considerations you’re talking about? What’s this whole conservation of number thing?” And Schubert was like “I dunno.”. And the math community said “What do you mean, you don’t know? You don’t have a proof?”. And he was like “Nah man, I don’t have a proof. I have the answer. Deal with it.”.

And they did deal with it. They had to, because he kept solving problems and he kept using these totally wonky methods and he kept getting the right answers. The thing that makes this story really weird is: lots of other people tried to get on this bandwagon, and tons of other people just couldn’t do it. They would do this whole simplifying assumption and try to do this whole “conservation of number” thing and they would just get completely wrong answers.

Eventually, the situation got so ridiculous that in 1900, David Hilbert wrote this as the 15th problem on his famous list:

The problem consists in this: To establish rigorously and with an exact determination of the limits of their validity those geometrical numbers which Schubert especially has determined on the basis of the so-called principle of special position, or conservation of number, by means of the enumerative calculus developed by him.

You can practically feel the frustration seeping out of these words, 117 years later.

Wikipedia lists this question as “partially resolved”. What is meant by this is, to this day, we still don’t really know what “conservation of number” actually means. Phrasing it in Hilbert’s language, we don’t understand the “limits of its validity”. However, in the end, people did figure out a way to do these computations rigorously, and so research interest in figuring out exactly where “number is conserved” has by and large died out.

I’ve already written a little bit about the technical tools which make this possible, but in the next post I’d like to talk about a high-level picture, and an “intermediate step” that I’d never really understood before.

[ Next ]

#math #maths #mathematics #mathema #history #math history #geometry #algebraic geometry #combinatorial geometry #schubert stuff

76 notes · View notes

chikachikatto · 5 years

Text

A history of Greek Mathematics

Ok so gunna briefly comment on this book by Thomas Heath.

So the book first starts out with some masturbation over how good greeks are about science and stuff. After that he goes on to give a bunch of expositions about how greeks have categorized mathematics + etymological tracings. I think one of the most notable part of this is him talking about some traces of the word ‘mathematics’. In Laws he notes that plato referred to arithmetic, measurement, and astronomy as ‘tria mathemata’. Basically 3 subjects that are fit for freeborn men. See, greek thinkers back then thought it was fashionable to do things most people now a days consider ‘intellectual masturbation’. We can see a similar notion talked about in Aristotle’s Metaphysics. In it he notes that the wisest men have knowledge that is detached by normal practical use. There’s also commentary about how these fields really arose when Egyptians and other such peoples gained the free time to do this stuff. I think while this is true, I think it is too hasty to adopt an extremely progressive view on the issue and imply scientific progress would speed up significantly if people had more free time. See, the thing is, the greeks back then didn’t have video games, porn, anime... No skinner boxes. Stuff was probably extremely boring for them. These intellectual pursuits were, amongst other reasons, so they do not experience brain rot!

Moving on... As said before, there was also talk about how mathematics is categorized. There should be some familiar names for most people, but there are a few odd terms too. For example, the contrast between ‘Arithmetic’ and ‘Logistic’. It’s a bit misleading because how we use the word ‘Arithmetic’ has changed. At the same time, if you have looked at what we have talked about last time, you should have a guess that when greeks talk about arithmetic, the mean Number Theory. Logistic however is like sick techniques for mental calculation. Honestly, most of the algorithms greek used back then haven’t really left us to this day.

There’s also ‘Harmony’ which is like musical ratios and stuff. ‘Optics’ which deals with how things look at different angles, mirrors and other cool stuff. ‘Stereometry’ is an odd term, but it really means like theoretical astronomy. Actually Plato talks groups it within his big 4 that are related to mathematics iirc (Geometry, Arithmetic, Harmony, Astronomy). For some reason greeks also sought to give ‘geodesy’ (measuring of surfaces) even though it is just geometry? Yeah it probably made more sense to them than it does to me.

Ok, so off to more mathy stuff too!

I think one of the first things that caught my attention is them talking about gnomons. Originally it is the idea of adding these little right angle shapes to a square to get a larger square.

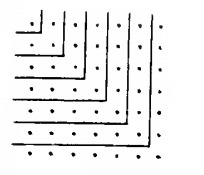
You can see clearly that it also gives a nice visual explanation for why the sum of odd numbers is always a square too! On top of that, you can pretty much generalize this idea to any shape you want... This is really pretty:

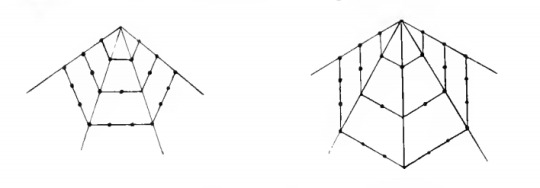
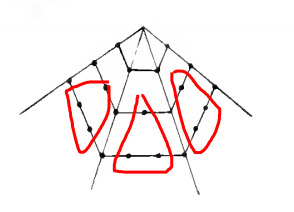
This also gave me an idea of how to re-derive the equation for polygonal numbers. First, let n be the number of the polygon. For instances for the smallest 5 dot pentagon, n = 1. Ok so we start with the ‘spokes’ each of which are going to be n dots long and there are s - 1 of them. Spokes can be illustrated like so:

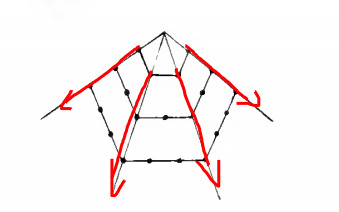
Next we have the filling triangles. These are (n-1)n/2 each and there are s - 2 of them. We can illustrate them like so:

Last there is the origin point from which the rays come from. Which is this:

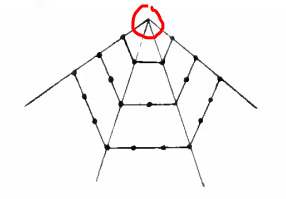
This finally gives us the general function for a polynomial number: p(n,s) = n(s-1) + n(n-1)(s-1)/2 + 1. Maybe there is a sexier way of counting it, but this was the first one I thought of. The reason why I thought of this btw was because I just had the need to derive the equation myself without any help. This was very pleasing to get at the end.

Ok more interesting math stuff. I’ve talked before about how the sum of odd numbers is a square, but something that blew my mind (though in hindsight is really obvious!) is that we can use this to get pythagorean triples. Heath explains how if we have some odd numbers 1, 3, 5, ... 2n + 1, if 2n + 1 is a square itself we can set it aside. Now if we add the number n^2 and 2n + 1, viola we get another square number! This is actually really obvious algebraically. Since we know that n^2 + 2n + 1 = (n + 1) ^ 2. An example of this in action is where we have the set {1,3,5,7,9}. 9 is a square so we take it aside. 1 + 3 + 5 + 7 = 16. Now 16 + 9 = 25. That’s pretty darn magical.

I think in reflection of this, it really shows how you can come up with some pretty interesting generalizations and conjectures if you have the right way of visualizing what you are playing around with.

A quick note I’d like to make is about one of the arithmetic statements Theon made that was included in this book - that for any number m, either m^2 or m-1 is divisible by 3, and either m^2 or m^2-1 is divisible by 4. The proof in the book is fine, though we can have an alternative proof that is far shorter:

First note: m^2 - 1 = (m+1)(m-1)

|Z : 3Z| = 3, so 3|m, 3|m+1 or 3|m-1.

One thing that was interesting metacognitively for me in writing down the proof above down is that it didn’t occur to me until just now that the number of possible ways a remainders a number has modulo n corresponds to the index of the subgroup nZ in Z. It’s odd because the examples I’ve seen of the index are always so abstract and unmotivated, but I just realized it is something that encodes a strategy I already use. Best part of formalization is that after encoding this strategy, you can then develop theorems and methods out of it to further your tool set.

I’m going to skip the musings about Egyptian mathematics. Instead, I will like to bring our attention to Democritus. Now, for whatever reason, Plato really hated this guy.

'If’, said Democritus, 'a cone were cut by a plane parallel to the base [by which is clearly meant a plane indefinitely near to the base], what must we think of the surfaces forming the sections ? Are they equal or unequal ? For, if they are unequal, they will make the cone irregular as having many indentations, like steps, and unevennesses ; but, if they are equal, the sections will be equal, and the cone will appear to have the property of the cylinder and to be made up of equal, not unequal, circles, which is very absurd.’

I genuinely wonder how wildberger or John Gabriel would respond to this problem. Though honestly, my guess is that they would without hesitation affirm the idea that the cone only consists of discrete steps. At the very least, it calls into question their pretensions that the greeks were allergic to the idea of infinity or infinitesimals. I mean, even Archimedes (who at least Gabriel likes very much) seemed to have helped influence the early ideas of the limit. Heath also notes that Democrats appears to have anticipated Archimedes’ work.

A quick more pedagogical observation I just made is with proofs. On my own, based on some readings I have done on fluid intelligence, I thought a good way to understand a proof is to break its main goal into sub-goals/modules. This not only allows for better understanding, but it also opens an avenue for high road transfer. Now my observation is similar to subgoals, but it is markedly different in a way that it deserves its own name. This is what I call a ‘scene’. For example let us look at a proof Hippocrates did of the lune. First of all he reasons about this particular figure:

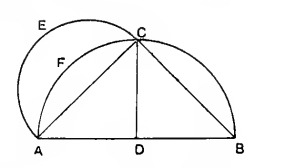
However, all of a sudden, he moves to a radically different figure afterwards:

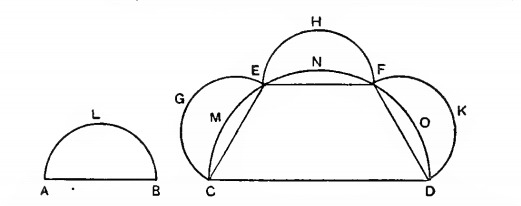
What is tying these two scenes together is a sort of ‘functorality’ that allows further progress in a result. From here there are multiple avenues. First of all, elaboration of the different scenes in a proof allows for better memory of what is going on. But it’s not just that. You could generalize the scene transitions and try thinking of problems that could use them. For example, I see here that the scene transition involves taking a piece of the first figure (the part with the semicircle and diagonal), and using it to form a regular shape that is then related to these lunes in a certain way. An analogous use of this scene transition could be if these diagonals instead had a right angle triangle, and we used that in a semi-hexagon (or really any other shape for that matter). What then?

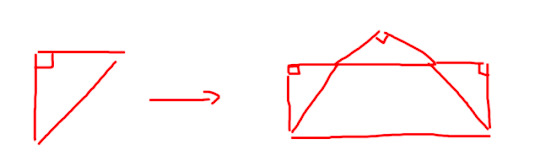
This could promote not just a transfer of general problem solving strategies, but also a transfer of insight. Admittedly the example I just illustrated is rather silly, and I think what really gives the scene transition its power is that the lunes share part of their area with the larger semicircle. This is just an illustration of the concept.

Now, I want to quickly talk about Euclid’s GCM (Greatest Common Measure... we’re with the greeks so measure=divide) finding algorithm which, if I do decide to read Book X of the elements, we will see again. It goes like this:

If, when the lesser of two unequal magnitudes is continually subtracted in turn from the greater [this includes the subtraction from any term of the highest multiple of another that it contains], that which is left never measures the one before it, the magnitudes will be incommensurable

This is worded really badly. In fact I had to search for a presentation that presented it as a computer program to really understand what it is talking about. Ok so suppose I want to find the GCM of a and b. So what I do is compare them. If a>b, then I take some a_2 = a-b. If b>a, then I take some b_2 = b-a. Now without loss of generality, let’s suppose a>b. Then after that I compare a_2 with b in the same way. This goes on recursively. We stop when some b_i = a_j = d in which case this number would be our gcd. If we can’t stop, then the two aren’t commensurable.

If you cared about such a thing, here’s the Haskell implementation of this algorithm

gcm :: Int -> Int -> Int gcm a b | a > b = gcm (a-b) b | a < b = gcm a (b-a) | a == b = a

If you are familiar the normal exposition of the Euclidean Algorithm, you might be confused why we aren’t using modulo. Well, if you think about it, we still technically are. If a>b, then we are subtracting b’s from a_i q times till we get to some r where we can’t describe anymore. This gives us the equation a = bq + r which starts to get familiar. With all that said, I haven’t gone to the part I’d like to discuss. Here is the image of it:

Basically what we do here is that we cut AB into the golden ratio at point C. I don’t know why but this looks really cool and is what happens when we continuously cut by the golden ratio. Notice how AC:CB = DC:AD = DE:EC and so on. It just keeps going. If we set AC = ϕ, then CB = 1. This then shows that ϕ has no common measure with 1, and thus it is incommensurable.

There’s also a geometric proof of sqrt(5) given (who’s original author was Zeuthen) where its visualization is very eye-catching and concise:

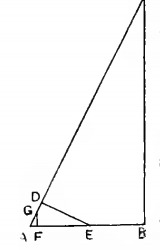
How it is proven that all these triangles are similar is really cool, though I prefer the calculation-based method as my spacial IQ is too low. On that note, I REALLY should have read some preliminary material, because some of the proofs regarding higher curves are near incomprehensible, as there are just things that are taken for granted that are not at all obvious.

I don’t think I have much Archytas’ works in my book collection, but I’ve seen his name enough that I might as well look at one of his results. What archytas want to do here is double the cube. At this time the greeks knew that we just have to find 2 mean proportionals to get our result. What does this mean? Well first we start with what it means to have one mean proportional. That means where a and b are the numbers we want to relate and m_1 is the mean proportional, a/m_1 = m_1/b. 2 mean proportionals means that a/m_1 = m_1/m_2 = m_2/b. More generally, mean proportions fit into a and b like so:

a/m_1 = m_1/m_2 = ... = m_n-1/m_n = m_n/b

However, you may ask, why is finding 2 mean proportions related to the doubling of a cube? Well let’s suppose b and c are 2 mean proportionals to a and d. This means that a/b = b/c = c/d. So now we do a little bit of algebra.

b/c = c/d => c^2 = bd => b = c^2/d(1) a/b = b/c => a = b^2/c => [sub in (1)] => a = c^3/d^2 => a/d = c^3/d^3

With this we see that if a = 2d, then c^3 = 2d^3, so we have a way of setting a such that we can then get a c that can be used as a side length to double the cube.

The question now is how do we get these mean proportionals? The way Archytas does it is to get the intersect between the tore (a portion of a torus in a certain way), cone, and, and cylinder. Since he was working with euclidean geometry, he had to give a rather complicated account of how all of these shapes are to be constructed. This is actually where the breakdown into scenes (as opposed to showing one massive messy figure shown in Heath’s book) does wonders for us to see clearly. Colours help too

First we have a circle ABC of diameter AC, and then we make some semicircle perpendicular to ABC but same diameter. For the tore, we are going to rotate this semicircle. around A as a pivot

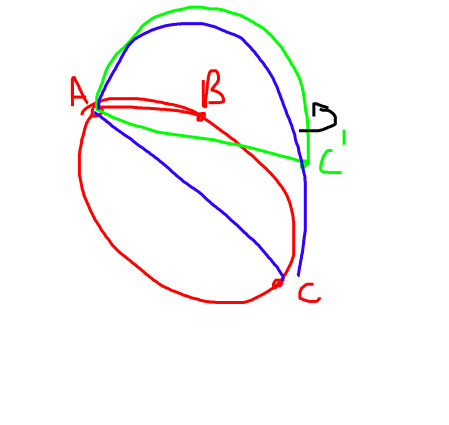
We also have a semi-cylinder using ABC as base.

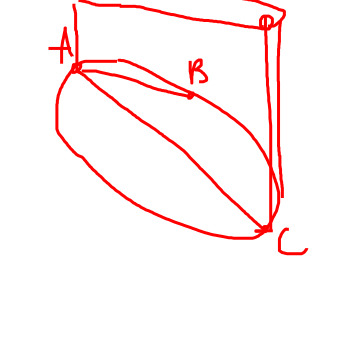
Lastly for the cone, we put a line through B and produce it to D such that there is a line CD that forms a right angle with AC. From there, we rotate this whole triangle around the axis of C to get the cone. It might seem hard to use the cone, which is why we also have a diameter BE perpendicular to AC. The semicircle made from this and perpendicular to ABC has the property of tracing our cone.

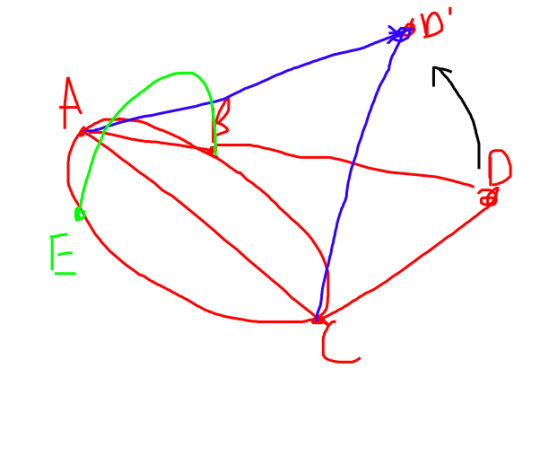
The end product is the rather complicated diagram provided by Heath:

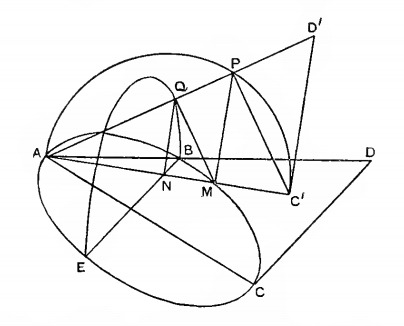
The rest of the story isn’t as important. From this construction, we observe the the following relation that:

AB:AP = AP:AM = AM:AB

WOW. This took me more time than I’d like to admit to understand! The main issue I had was keeping track with all of the operations. Euclidean Geometry is based on rather simple to understand rules as particulars, however the sheer mass of relations you need to keep track of gets tiring.

Something we can notice, is that part of this proof is to show that M must be on the circle. For it intersects the surface of the semi-cylinder with the circle as the base. This means that we could’ve just projected the intersection of tore and the cone. Tannery gives such a solution. Honestly, it is really neat since you have to look at way less relations, but at the same time I don’t feel like showing it. What it basically shows that a certain euclidean construction sort of encodes this projection.

While I am still thinking of how I suck at following these proofs, Heath also provides a rather famous quote of Menaechmus:

‘O king,' said Menaechmus, ' for travelling over the country there are royal roads and roads for common citizens, but in geometry there is one road for all.'

Though in a sense if you really want a short road, you’d refer yourself to Descarte’s geometry that simplifies a bunch of stuff. Actually after just noting the previous method, I didn’t realize that in some sense Menaechmus anticipates descartes. For his own solution of two mean proportionals, he used the intersections of parabolas of hyperbolas. Using our modern notation, this is in some sense obvious. For if we have a/x = x/y = y/b, then:

a/x = x/y => y = x^2/a (parabola 1)

x/y = y/b => y^2 = bx (parabola 2)

a/x = y/b => xy = ab (hyperbola) (we can arrange and get y = ab(1/x) for a familiar looking equation)

Though it is fascinating that Menaechmus seemed to have knowledge of these geometric and arithmetic relations.

Of course, with all these solutions, Erasthothenes probably has the best one. Basically you have a mechanical contraption of movable triangles like so:

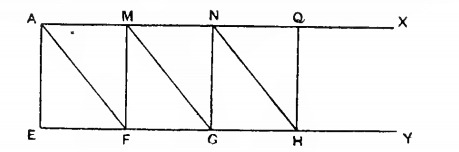
Then we slide the different plates so that B, C, and D are all in a straight line like so

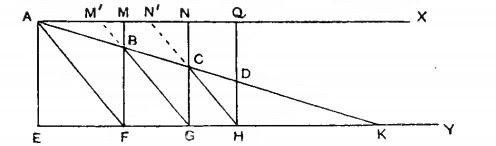
Now EK:KF = AK:KB = FK:KG. EK:FK = AE:BF and FK:KG = BF:CG. This means that AE:BF = BF:CG. For the same reason, BF:CG = CG:DH. This means that AE/BF = BF/CG = CG/DH. Where BF and CG are the 2 mean proportionals of AE and DH as required.

Something I didn’t note, because I am sort of hesitant to show an example, is how the greeks tended to use inclinations. Basically they’d often create constructions where they had a very particular relation to each other. For instance, the following figure is constructed such that GH=FD:

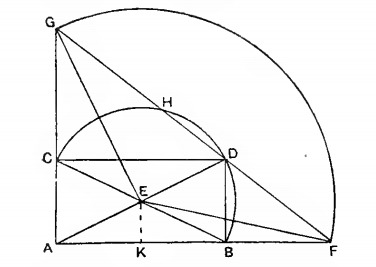
The way they often use to get this measurement just right is then to use a curve. In this instance, one could set D and H by finding the intersect between a particular hyperbola intersecting the circle CHDB. Now, this was supposed to be another instance of doubling the cube, so we can just use the equations of the mean proportions before. Namely

ay = x^2 (1)

y^2 = bx (2) and,

xy = ab (3)

If we add (1) to (2) we get x^2 + y^2 - ay - bx which corresponds to our circle. Meanwhile xy = ab corresponds to the hyperbola in question.

Now unto the philosophy of plato. One thing that has been going on since me writing this is that I would be in this odd time loop in which I’d read this section of the book, look for studies investigating it empirically, and by the time I realize I can’t find any, I forgot what I was reading. Anyways, what we must first note is Plato’s philosophy about mathematic’s ethical relevance. To him, mathematics was not just a tool, but also a practice that helped elevate man to the Good. It was something that trained the mind to look toward eternal truths as opposed to lowly earthly things.

This then raises the question of why he’d include astronomy and harmonics as studies, because these seem like products of our material world. As Heath noted, Plato’s response would be that the heavenly bodies and the string lengths corresponding to the mathematical models of these disciplines aren’t fundamental. Rather they are merely imperfect representations. When we are talking about astronomy, we are really talking about kinematics, i.e. the mathematically described perfect movement of these bodies.

Plato pushes this idea to suggest a division of the different things when we talk about when referring to the mathematical objects. For instance, with triangles we have physical instances of them. We also have the name, and definition of them Lastly we have the idea of the triangle - the absolute mathematical object. He maintains that we may illustrate mathematical objects and their representations, but the absolute object is only conceivable in thought. This would suggest that while we have various representations of these concepts, the truth of the actual object in itself can only be arrived through thought. This would naturally take us to Kant who’d maintain that empirical truth is also possible. As a counter-argument he’d point out how our ideas of geometry are are still based on phenomenal intuitions. This would mean that mathematical objects don’t actually take us to noumena but we are still within the scope of our phenomenal world.

This also in turns provides a problematic for speculative realists. If mathematics can describe reality beyond what is conditioned by thought, where does mathematical syntax fit into the picture? Does go back to a noumenal feature of reality that our minds can still grasp? How would one separate themselves from an almost absolute idealism if that is possible or preferable? I’m guessing there are theoretical tools like that of Laruelle’s that help us think about this. I might want to meditate on this more sometime... Or actually put time into reading Brassier’s work.

You will notice I am skipping a lot of Eudoxus’ work however one part of it caught of attention, namely the theory of concentric spheres. Basically each heavenly body had 3-4 spheres concentric to each other that then affected the position of the body. Think of a gyroscope. The first dealt with how long it took for the bodies to get the same position with respect to the stars every 24 hours (sidereal). The second dealt with the movement of the body around the earth’s ecliptic axis every year (zodiacal). The third dealt with the time it took for a body to reach the same position with respect to the sun (synodic). The last one rotates relative to the third sphere but in the ‘opposite sense’ whatever that means. I have to admit my incompetence here. What I do take from this is that the 3rd and 4th sphere can then be combined into a ‘hippopede’ which is basically an infinity shape lmao. This shape can be also gotten by the intersection of a cylinder with the 3rd sphere like so:

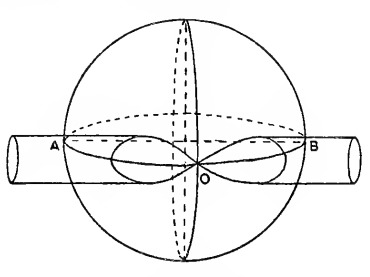
Something I like about this is how methodical this model is. Eudoxus just noticed a bunch fo patterns and made a sphere that dealt with each one. Is it accurate? No. Is it easy to work with? No. However, it is something where you can easily see where he is coming from. One thing this creates is a rather fine implementation of the oscillations between accelerating and slowing motions of the planets.

Something I want to give a brief account for is the distinction between analysis and synthesis. Heath asserts that Euclid’s exposition is mainly synthetical. Generally, synthesis is working from knowns to unknowns. Meanwhile analysis comes from distilling something unknown to something that is known. You can easily make a comparison between this and analytical and synthetical propositions, but as you might notice the two notions are similar, but not actually the same. For Kant, analytic propositions make tautological claims that are based on the concept itself. Meanwhile a synthetic proposition adds to the concept. He’d say for instance that 2+3=5 is a synthetic proposition which seems rather strange.

The similarity lies where analytic propositions in a sense reach into the inner-conception of the object, while analysis reaches into the deeper crux of a problem. However, the difference lies in the fact that it is debatable whether or not any crossroad we reach when analyzing a problem can be said to be immanent to the problem itself. For instance, when we reduce the question on the irrationality to root 2 to a question of the prime factorization of squares, it isn’t clear that prime factorization is immediately involved in the question of square root 2′s irrationality. This should lead us to believe that analysis of mathematical problems still gives us synthetic propositions. On a tangent, Heath notes that reductio ad absurdum is a form of analysis as it reduces the problem to a statement we know is false.

Anyways I think that’s it for now. The rest of the stuff is related to Euclid which if I keep writing, will talk about some other time.

Edit: Quick note, almost forgot to provide a list of the different types of questions in greek mathematics. The first is for theorems where we are proving a hypothesis. There also comes problems in which we are trying to construct a shape. Porisms appear to be the case where we have an ‘incomplete theorem’ expressing a certain lore where we need to figure out what else is needed to connect the dots. Lastly there are diorismos questions in which we are trying to delimit the space of values that can be put into our functions and get a valid solution.

0 notes