javas-maths-blog

[javas-maths-blog]

Lets get imaginative part 2

Referring to the tidbit from last post. It might seem unintuitive for R * e ^ (i * theta) to be able to calculate points. This is because of the core property of e being the number raised to the X power will be the derivative of itself. This makes it have interesting properties when raised to the i power. You may have heard of e ^ (pi * i = -1). Well it can be defined even further.

E ^ (theta * i) is equal to cos( theta ) + i * sin( theta )

But why is that.

Well, first we have to more rigorously define the power function because the general description only applies to integers and mixed numbers.

A ^ B is written as A * A *... [repeat B times]

But this can also be written in the form with the exp function

Exp( A ) is equal to e^A

But that isn't correct yet, we need to add our secret sauce

Natural log

This is the reverse of raising e something power, so our equation would look like this.

So A ^ B is equal to exp( B * ln( A ) )

So exp( ( theta * i ) * ln( e ))

And ln of e is 1 so we can cut that part out

So we are left with exp( theta * i )

It may seem like we just made a necessary step but this is to prove that e is the constant that helps us take apart the power function, any other value wouldn't return itself.

Bam, we just redefined powers!

Now we are stuck with theta * i, no problem, it graphs a vertical line.

So where doe e come into play?

Lets graph a few points

https://imgur.com/a/LscTdh1

As you can see, this matches a cosine curve when plotted on the real axis and a sin curve on the imaginary axis

So with that under our belts, we can finally match the cartesian coordinates to polar coordinates

e ^ ( theta * i ) is equal to cos( theta ) + i * sin( theta )

However, this only defines our unit circle, we still need to multiply it by R so it stretches to the point we desire.

The reason e is useful here over any number is that it undoes the ln function in exp( B * ln( A ) ) so it returns itself, let's look at that.

Imagine the number e is raised to as a distance you are walking around a unit circle, it follows the path of a circle perfectly.

But why?

Well lets try using a number instead of e and take its derivative

That slope is how the absolute value changes when theta gets larger

If it is less than e, it shrinks over time, and if it is larger than e it gets exponentially larger as theta increases.

At the value e the d/dx of exp( n * ln( x ) ) is 1 but for any other value it quickly diverges from the straight line.

So if we were to plug in another number it would spiral in a similar fashion as e but it’s absolute value would change .

[javas-maths-blog]

Let’s get imaginative

Back in middle school, you were told to never square root a negative, just write “no solution.” however, this is not the case. It simply leaves the plane. The square root function denotes “what times itself is equal to the number acted upon.” but a negative times a negative is a positive. The solution is simple, replace the unknown with a variable, i.

The concept of i started when bankers were faced with a dilemma, there was no way to compute debt in a non-lossy function. This means that if they were not careful, money could appear or disappear from banks. And thus, i was created, seemingly out of thin air. It is only years later that i’s true potential beyond just a workaround for a specific problem.

Before we get right into this, lets go over the basics of i.

Complex numbers are written a+bi format. So sqrt(-2) would be written as 0-2i

You can remove a part if it is zero.

Also we treat i like an x, so it gets parsed LAST

Let's start with one of the most common functions done to complex numbers, squaring. We use the age old acronym FOIL or First Outside Inside Last. so let's do the function (2+3i)^2

First, expand it (2+3i)(2+3i)

Then, split it into the FOIL commonents

F: (2 * 2) -> 2 ^ 2)

+

O: (2 * 3i) -> (0 + 6i)

+

I: (3i * 2) -> (0 + 6i)

+

L: (3i * 3i) -> (3 ^ 2) * (i  * 2)

|

V

(2 ^ 2) + (0 + 6i) + (0 + 6i) + ((3 ^ 2) * (i  ^ 2))

{note: i^2 is -1}

|

V

(4) + (6i) + (6i) +(9 * -1)

|

V

(4 - 9) + (12i)

|

V

(-5 + 12i)

So therefore

(2 + 3i) ^ 2 = (-5 + 12i)

Using I can get quite cumbersome very quickly. That is if you only view it algebraically. It an be explained graphically, in fact, it is explained better through graph.

Complex numbers can be graphed by treating the real and imaginary portions into cartesian coordinates. So (1 + 2i) would plot to (1 , 2).

On the real plane, we can graph sqrt(x) and extend the i plane in the z direction, so sqrt(x) now looks like this https://thumbs.gfycat.com/PoliteOptimalBaleenwhale-mobile.mp4

The next major function got complex number is the absolute value function. Now, if you were to view it algebraically, it may seem intuitive to simply make the current value only positive, but that  is not how it is solved.

Absolute value do not denote “positive” but instead denotes “distance from (0 , 0).”

Since complex numbers can be defined by point, we simply have to create a line from 0,0 to a,b and calculate the distance. Let's take the complex number 4+7i.

4 + 7i

|

V

sqrt( 4 ^ 2 + 7i ^ 2 )

|

V

sqrt( 16 + 49)

|

V

sqrt( 65 )

|

V

32.5 * sqrt( 2 )

Now for the extra little bit, we can express imaginary numbers with a different method. It looks more complicated but can be used for calculus since it is expressed in a way where taking the derivative is easier.

It can be expressed by C = R * e ^ (i * 2 * pi * theta ) where theta is a value between 0 and 1

Theta is the angle from (0 , 0)     and R is what the absolute value of the the point.

[javas-maths-blog]

Transformation and conversion with socahtoa

So, from the previous post we discussed the trig functions alone, but combined they hold great power. It allows us to find information about unknown values with seemingly arbitrary information.

For example, we can find the angles of a right triangle with just lengths

THIS is where sohcahtoa comes in:

Sin Opposite

Hypotenuse

Cosine

Adjacent

Hypotenuse

Tangent

Opposite

Adjacent

Which can more accurately be expressed as:

Sin (theta) = Opposite divided by Hypotenuse

Cos (theta) = Adjacent divided by Hypotenuse

Tan (theta) = Opposite divided by Adjacent

To solve this starter problem, first let’s define our points, A is 0,0, B is 0,1, and C is 3,0. Next Pick any line on the triangle where we know its length and it creates the 90 degree angle, (so not the hypotenuse). Lets chose the one from points A to B. since it will be length 1 for easy calculation. That line chosen is our adjacent, making the other one our opposite.

We now have

Adj = 1 unit

Opp = 3 units

Hyp = ? units

Angle A = 90 degrees, Angle B = ?? degrees, Angle C = ?? degrees

Where angle B + angle C must equal 90 since all triangles must have their angles add up to 180.

Since we have line AB (Opposite) and line BC (Adjacent) but not AC (Hypotenuse), we will use Tangent.

The formula will be expressed as so:

tan(theta) = ⅓

Now we bring our great friend the inverse function along. We perform it to both sides giving us:

tan^-1(tan(theta))=tan^-1(⅓)

Theta = tan^-1(⅓)

*make sure you are in degree mode :)

So tan^-1 mean “what angle returns the value tan is acting on”

We can split tan into sin/cos

Sin(x)/Cos(x) = ⅓

This part we will skip for now because it involves things to the power of i

So it approx equal 71 degrees

From this getting the rest of the angles is trivial simply add 90 to 71 and have it subtracted from 180, giving us 19

Now we have all of the angles of the triangle!

Since the furthest point is 3 units away, this also creates a unit circle of radius 3.

We can also turn angles into length, let's use our ending values of A = 90, B = tan^-1 ⅓ and C being 180-(A+B)

We need the length one one line, for the radius. To now its tan(B)= X/3

Form there, we run the tan^-1 and we get

tan(tan^-1(⅓)) =(x/3)

So ⅓ = x/3

Therefore x is equal to 1

Using angles to find distances had many real life applications. surveying land for plots often requires complex calculations in order to get the information needed for surveying land.

This often comes into play when dealing with rocket science. With such a limited view \ and such far distances, you take all information you can get. This becomes even more crucial since the room for error is so strict that miniscule miscalculations can lead to catastrophic failure.

[javas-maths-blog]

The triggy bois

NOTE:

For this lesson we shall be degrees over radians, to convert degrees to radians, calculate

(Theta / 180) * pi

Today we are going to go over the trig functions and their counterparts

Before we start, lets list the functions we hall cover

Sin, Cos, Tan, Csc, Sec, Cot, Sin^-1, Cos^-1, Tan^-1, Csc^-1, Sec^-1, Cot^-1, Sin^2, Cos^2, Tan^2, Csc^2, Sec^2, Cot^2.

This may seem like a lot, but the way they relate to each other is quite intuitive, so just hang on.

Let's start with the basic two

Sin and Cos

Imagine a circle with radius 1, with a radial line that is 45 degrees from center to edge.

For this you can find what point the end lies on.

You would plug in cos(45) to get the X cord and sin(45) to get the Y cord.

For this example, they both come out to sqrt(2)/2

While this example may seem to suggest sin and cos are the same, they are in fact not. They output the same values at only four unique angles, 45 degrees, 135 degrees, 225 degrees, and 315 degrees. (this is given that the angle is already parsed through the modulo function of 360 degrees [mod(x,360)] as adding 360 degrees does not change the angle relative to the origin angle)

However Sin and Cos are very similar as Sin is simply an offset of Cos by 45 degrees. So Sin(x+45) is equal to Cos(x).

Another way to think of sin and cos is to use the Pythagorean theorem, or a^2 + b^2 = c^2

Where Cos is the a, and Sin is the B and theta is the angle of C.

Now that we have the basics, lets go off on a tangent, with tangent (this is relevant and not a tangent). Tan is expressed as (Sin / Cos) and represents slope of the line tangent to the circle given the point specified at (Cos(x), Sin(x))

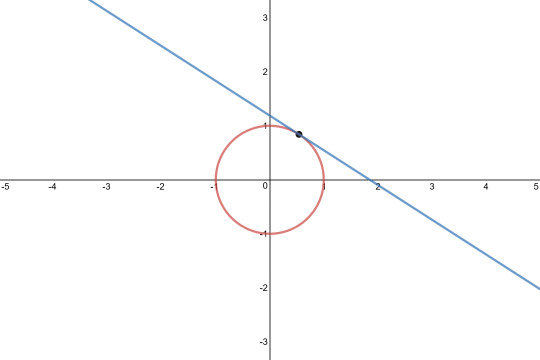
Now we have the core ideas of sis cos and tan, we can have some fun with them.

First, lets cover the evil twins of the trio: Csc, Sec, and Cot.

Before the relationship, we must clear up a common mistake, Cos connects to Sec and Sin connects to Csc. This is unintuitive due to the the prefix “Co” that cosine and cosecant share, but they don't match.

Sin connects to Cosecant.

Cosine connects to Secant.

Tangent connects to Cotangent.

They connect to their respective functions by raising said function to the power of -1.

So:

1/(Cosecant) = Sin

1/(Secant) = Cosine

1/(Cotangent = Tangent

This means Cotangent also = Cosine / Sine

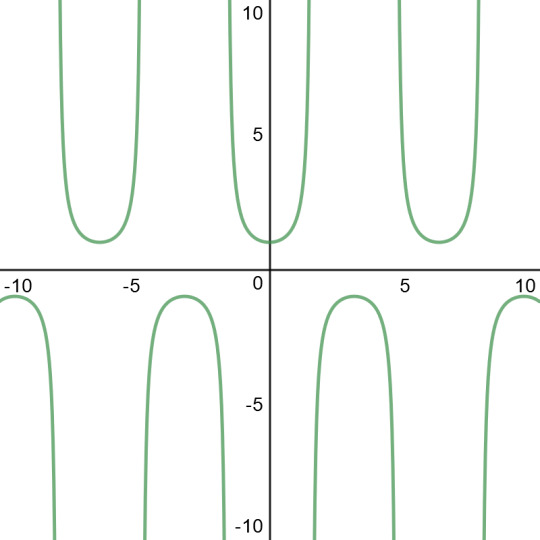
Next is the inverse functions, this will transform the cartesian coordinates into its theta angle.

It is expressed by placing a ^-1 inbetween the function word and its parentheses.

NOTE: the ^-1 functions DO have bound limits where the function fails.

sin^-1(x): -1 <= x <= 1

cos^-1(x): -1 <= x <= 1

tan^-1(x): x = [ALL REAL NUMBERS]

csc^-1(x):  x >= 1 or x <= -1

sec^-1(x):  x >= 1 or x <= -1

cot^-1(x):  [ALL REAL NUMBERS]

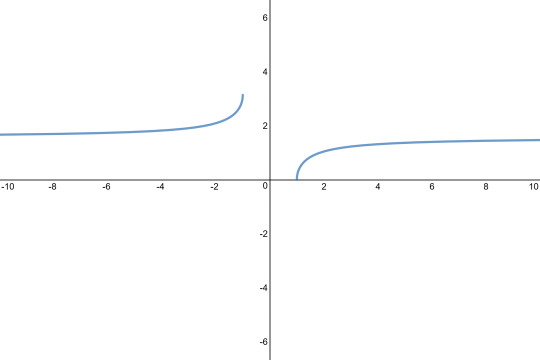
Lastly is the ^2 functions, they do not have bound limits, you simply square the function

Sin^2(x) = Sin(x)*Sin(x) or Sin(x)^2

And so on

This concludes the basic triggy stuff.

#math #trig

[javas-maths-blog]

water, fire, air, dirt, freaking fractals how do they work

Fractals and other things with iterative functions

(this is a family friendly math blog)

One of my favorite things in math is to make and experiment with in matn are iterative equations. I like the idea of changing something so small to a simple function and it producing a wildly different result.

While not iterative itself, a way to get started into iterative functions is to look at summation, which an be expressed by capital sigma (Σ). Sigma notation is expressed as shown below:

https://imgur.com/a/oPweQxt

First pick a variable, we will use n for this example, it is placed on the bottom left corner. Then, choose your starting value, set n equal to it. Then choose your ending value and place it on top. Finally place your function of choice in front of the Σ.

Summation said verbally is “from n equals zero to 10, 2^n +1”

Let us calculate the function below.

https://imgur.com/a/mhSmu0H

This is equal to (1/(1+0))+(1/(1+1))+(1/(1+2))+(1/(1+3))+(1/(1+4))+(1/(1+5)).

You add the function to the left to itself for all values of n.

This is equal to 1+½+⅓+¼+⅕+⅙ or 2.45.

On a tangent, the multiplication version is represented as a capital pi. (Π)

Before we head to iterative functions, note that the ending value can be infinity. Summation problems that end like this can have surprisingly and seemingly paradoxical answers,like the famous 1+2+3+4+... = -1/12 but this is better left for another post.

With this under our belt, we are ready to tackle iterative functions.

Let's start with a self similar one (picture below) the equations from this point on are too long for explanation in text form, so they will be in the imgur links listed when referenced.

https://i0.wp.com/joedubs.com/wp-content/uploads/2015/11/fibonacci-equation.gif?fit=500%2C290&ssl=1

This function approaches the value (1(plus or minus)sqrt(5))/2 when continued.

Now with a brief look at our golden boy phi, let's get imaginative.

The Mandelbrot function requires a complex input (formatted as a+bi).

Z1=Z2^2+C

When starting Z2 is zero, and C is your input.

Once done, plug your answer back into Z2 and add C again, repeat this indefinitely.

Depending on your input, your number has done one of two things

A) Blown up to a very large number

B) Stayed quite small

This is no coincidence, whenever the absolute value (| |) of your number exceeds two, it will blow up. However, some numbers stick around longer before leaving this threshold, while some stay forever. With all points mapped “inside” the set (not blowing up) it would look something like this:

https://imgur.com/a/4k8JaDl

https://imgur.com/a/D4gfHks

This is what is known as a fractal, no matter how far you zoom in, the shape does not get smooth.

As explained by 3Blue1Brown, “it’s a rebellion against calculus”

Fractals exist in a bizarre realm were infinite values are commonplace.

Like a question asked prior, this shape has a finite area and an infinite perimeter.

[javas-maths-blog]

Truncation and modulation

Truncation and modulation are some of my favorite functions as it can be used as a to format unpredictable numbers into easy-to-use segments.

Truncation involves cutting off a number’s digits at a given point. For example truncating the number 𝝿 at 0.01 returns 3.14. The remaining digits are discarded. This can be expressed in three ways in the terms of functions: Floor(x), Ceil(x), and Round(x). Floor(x) disregards all numbers beyond the integer position and rounds it down. Ceil(x) does the opposite, rounding decimals to the integer position, for example: Ceil( 0.0000...1 ) = 1. Round(x) is a combination of floor and ceil, if the decimal is greater or equal than five, it rounds up, otherwise it rounds down. This can be applied graphs, which are often called step functions. The pictures shown below are examples of the Floor Ceil and Round functions applied to f(x) = 2 * sin(x). The graph is marked green when the modifier is greater than the parent and red when it is less.

https://imgur.com/a/BsFCgIL

https://imgur.com/a/KqNEIls

https://imgur.com/a/NSmX48b

You can also modify how the step functions work by changing what is done to x inside of the parentheses. For example f(x) = (Floor(10 * x) / 10) will round the number to the first decimal position instead of the integer position. It is important to note that any changes done to x inside of the step function must be undone by its inverse operation outside the function.

https://imgur.com/a/ZBXCTFG

https://imgur.com/a/CRUMFhn

Step functions can be used for smoothing out seemingly very complicated graphs into more digestible pieces by removing points to clean it up.

https://imgur.com/a/rQmNr3u

https://imgur.com/a/9MNjoRU

Modulation is similar to truncation as they are both step functions, however they play a different role. Modulation is a way to find the remainder of a number in respect to another number.

For example mod(4, 7) = 3. Remember back to elementary school when you first learned to divide (I know, painful), when you divide you got an integer solution and a remainder. Modulo is like dividing and truncating the dividend and leaving the remainder. The function mod(x , 2) would look like this.

https://imgur.com/a/zxVJ0OK

Unlike the normal truncation functions, modulo functions cannot be nested indefinitely to the same result. It gets quite crazy.

https://imgur.com/a/IyKXRXk

A good way to imagine the modulo function is like a sideways pac-man board, where the top and bottom are “warp points,” going through one warps you to the other. These “warp points” are a distance of what is specified as the second number in the function

https://imgur.com/a/EuhNHId

When displayed graphically, use of the modulo function like mod(x , (function)) is a more intuitive way to visualize its change over slope over longer distances. For the example below, the function 2^x.

https://imgur.com/a/8H8YZE5

Modulo is also used in the famous “self referential formula” as a means of looping the function back on itself without distorting the graph. In the graph, “⌊” represents the floor function (“⌋” represents closing the function, floor(x) can be written as ⌊x⌋)

https://en.wikipedia.org/wiki/Tupper%27s_self-referential_formula

Step functions are more than a step in the right direction.

#math #mathematics

[javas-maths-blog]

What is the square root of pi rounded to the nearest 100th divided by 15 times 89 minus 12

((sqrt(pi)*89)/15)-12 = (approx)-1.4834404846272715713642062655092052487345398936738363725980737802060597114265423905086261033513016518

[javas-maths-blog]

What’s the square root of 2*0+2*2?

Depending on how you want to define your parentheses, it can expressed as the following.

Sqrt((2*0)+(2*2)) = 2

Sqrt(2*(0+2)*2) = 4sqrt(2)

Sqrt(2*0) +2*2 = 4

[javas-maths-blog]

Can a closed object have an infinite perimeter

An enclosed object (assuming you are referring to a two dimensional plane) can have an infinite surface area. These are often called fractals. They can be either self-similar or chaotic. The Sierpinski triangle is one of my favorites. It’s perimeter is infinite, and it’s area is zero.