#eigenspace | Explore Tumblr Posts and Blogs

edvardsengrace26 · 1 year

Text

Shared Has a bearing on about Intimidation Perpetration and also Material Make use of Amid Young people in america

All of us proven the practicality involving using the transvenous remaining ventricular epicardial means for anti-bradycardia pacing, which can be employed if the trans-tricuspid strategy is not suitable.Frontalis insides with the use of the rubber elastomer is probably the preferred procedures LY-3475070 in vitro regarding repairing moderate-to-severe ptosis together with bad levator function. This process necessitates the add-on from the upper eyelid towards the frontalis muscle by way of a silicone chuck. Although this surgery may be carried out for many years, specifics of long-term outcomes along with issues is relatively restricted. All of us report a clear case of orbital inflammation Many years after a frontalis rubber sling insides operation pertaining to hereditary ptosis.Many of us statement the case of your 19-year-old lady with a combined hamartoma of the retinal pigment epithelium as well as retina as an aside discovered during her very first eyesight assessment. By way of this situation, many of us identify as well as illustrate the particular epidemiological and specialized medical traits in the condition as well as probable problems. (C) 2013 Elsevier Masson SAS. Most legal rights set aside.Elimination participation can be frequent within hematologic malignancies. It really is linked to adverse outcome as well as remedy issues. It could affect every area in the renal parenchyma (tubules, interstitium, glomerulus, vessels). A variety of mechanisms may be implicated: build up of immunoglobulin fractions or crystals, kidney infiltration simply by cancerous cellular material, urinary system blockage, paraneoplastic or perhaps storage space glomerulopathies... Diagnostic method relies upon the scientific presentation: acute renal malfunction, continual renal illness, glomerular proteinuria with or without nephrotic malady, tubular proteinuria, hydroelectrolytic disorders. On this evaluation, many of us depth the actual medical tests needed for the discovery and the follow-up of renal participation throughout hematologic malignancies, and also make clear your signs and symptoms of kidney biopsy. We advise analysis tricks of kidney participation within myeloma, Waldenstrom's illness, top quality lymphomas and also serious leukemias, poor calibre lymphomas and also continual leukemias. Your uncomfortable side effects associated with treatments (radiation, radiotherapy, stem mobile or portable graft...) are not dealt with in this evaluate. (D) The year of 2010 Societe nationale francaise p medecine interne (SNFMI). Published by Elsevier Masson SAS. Most rights set aside.One of the right now normal methods of semi-supervised learning would be to create a large sizing files as being a subset of an minimal dimensional beyond any doubt embedded in a higher dimensional normal room, and make use of forecasts from the files about eigenspaces of the diffusion guide. This kind of document is actually determined with a recent function regarding Coifman and Maggioni on diffusion wavelets to accomplish this sort of forecasts around employing iterates in the warmth kernel. In greater generality, many of us think about quasi-metric measure place By (instead of the manifold), as well as a really basic owner Big t outlined about the form of integrable features on By (in place of your diffusion map). We produce a manifestation of functions on By with regards to linear mixtures of iterates of To.

0 notes

ebouks · 2 years

Text

Algebra liniowa i geometria 3rd edition

Algebra liniowa i geometria Andrzej Herdegen eigenspace = przestrzeń własna To jest przestrzeń własna operatora liniowego: Ker (A – λ id) ≠ {0}, a poniżej jest przestrzeń własna Andrzeja Herdegena, fizyka matematycznego z Uniwersytetu Jagiellońskiego. Zakład Teorii Pola, Instytut Fizyki UJ, version 26 Mar 2018 Podręcznik zawiera rozszerzony materiał kursu algebry liniowej i geometrii prowadzonego…

View On WordPress

0 notes

nostalgebraist-autoresponder · 2 years

Text

Today's math post I can't write down rn because I'm procrastinating by sleeping.

more A simple argument about the existence of solutions to certain PDEs (heat equation, Dirichlet eigenvalue problem, etc.) seems to suggest there should be an eigenfunction in this sense, in some sense the only one (it would have to be odd and periodic, since the eigenspace is two dimensional, but there could be other eigenfunctions with different eigenvalues, I suppose).

This is kind of weird because it seems like a "toy" (small-scale, 2D, nice to visualize, etc.) problem but I can't figure out how to generalize it.

So the questions I'm asking myself are:

How exactly do the usual theorems about eigenfunctions of differential operators relate to this? Is the existence of solutions to these simple, 1-dimensional PDEs really just a special case of some more complicated, 3+1-dimensional operator? Are there more general results?

How do the usual proofs, like the Dirichlet eigenvalue theorem, go? Why can we reduce to proving that the eigenfunctions are orthogonal to the "wrong" solutions of the Dirichlet problem? I can't figure out the connection between these two things.

#mathpost

5 notes · View notes

weirdletter · 4 years

Photo

Phantasmagoria Magazine, Issue #16, edited by Trevor Kennedy, Phantasmagoria Publishing, Late Summer 2020. Cover art by Randy Broecker, internal illustrations by Franki Beddows, Randy Broecker, Dave Carson, Mike Chinn, Stephen Clarke, Peter Coleborn, James Keen, Allen Koszowski, Reggie Oliver, Jim Pitts, GCH Reilly and David A. Riley. Info: amazon.com.

Randy Broecker! Ramsey Campbell! Richard Chizmar! Interviews with Malachy Coney, Anna Taborska, Douglas Tait and Mathew Waters! Plus: Elak, King of Atlantis with Adrian Cole and Jim Pitts, Stephen Jones’ The Best of Best New Horror: Volume Two, The Phantom of the Opera, Psycho, Jaws, Candyman, Quatermass, Beneath the Planet of the Apes, Twilight Zone, Before You Blow Out the Candle... Book Two, 1970s horror films, R. Chetwynd-Hayes, fiction, artwork, reviews and more!

Contents: A Note From the Editor by Trevor Kennedy Randy Broecker interview and portfolio Ramsey Campbell interview Richard Chizmar interview (including reviews of Gwendy's Button Box and Gwendy's Magic Feather) The Many Faces of... The Phantom of the Opera: feature by John Gilbert Vic and Son: cartoon by James Keen Phantasmagoria at The Secret Bookshelf: feature with Trevor Kennedy and GCH Reilly Meanwhile, Back in Atlantis: feature by Adrian Cole, with artwork by Jim Pitts and review of Elak, King of Atlantis by David A. Riley Anna Taborska interview (including illustrations by Reggie Oliver from Anna's new book, Bloody Britain) The Fundamental Power of Psycho (1960): feature by Barnaby Page Jaws, Forty-five Years Later: feature by Barnaby Page Resurrecting the Candyman: feature by Michael Campbell Phantasmagoria Fiction: "Eigenspace X" by Mike Chinn "Hanuman" by David A. Riley. "Liver and Bacon" by Joe X. Young "Beady Eyes" by Barry Bellows "Shadow of an Incubus" by Christopher Fielden "Tomatoes According to Geoff" by D.T. Langdale "The Discontinued" by Jessica Stevens "Wolf Hill" by Sean O'Connor "He Thought He Was Dying" by David A. Riley "Towak" by Richard Bell "Three Sure Sentences" by Emerson Firebird Introducing Before You Blow Out the Candle... Book Two: with Marc Damian Lawler Malachy Coney interview Quatermass and the Kid: feature by Raven Dane. Beneath the Planet of the Apes (1970): feature by Dave Jeffery Twenty-first Century Twilight Zone: feature by Abdul-Qaadir Bakari-Muhammad Douglas Tait interview Mathew Waters interview 1970s Horror Films: feature by David Brilliance Reading R. Chetwynd-Hayes with Marc Damian Lawler Phantasmagoria Reviews Readers' Comments Acknowledgements

#magazine #phantasmagoria #weird fiction #horror fiction #dark fiction #weird reviews #horror reviews

15 notes · View notes

windyfiend · 4 years

Note

✨ eigenspace, latex, broccoli

“Don’t touch it!” Rodney slapped Sheppard’s hand away before he got too close to the plate.

“Ow!” Sheppard made a show of shaking out his hand. “What’s your problem? It’s just broccoli.”

“It’s not just broccoli.” Rodney huffed, offended on behalf of the little green floret that lay alone and spotlighted on a plate. “This broccoli was coughed up by that...” he flustered and squinted, “...thing in the cavern--”

“The potoo lizard?”

“--and luckily I had a pair of latex gloves in my bag because--”

“Why were you wearing latex?” Sheppard scrunched his nose, horrified. “Where did you even get latex? Didn’t they stop making that in the 30′s?”

“Latex,” Rodney hissed, “is the perfect material to contain and handle multidimensional objects. This piece of broccoli,” he gestured stiffly, “exists in the eigenspace of a complex matrix of variables that shouldn’t be physically possible.”

“Broccoli exists in a bunch of dimensions at once.” Sheppard’s voice fell dull and skeptical. “Is that why it gave me stomachaches as a kid?”

“If you ate this you would probably implode. Or explode. Or turn to bits of dimensional dust. I’m not sure yet, I’m running tests--”

“You’re gonna engineer a broccoli bioweapon?”

Rodney snapped a latex glove at his wrist, reached out with delicate fingers and gently lifted the broccoli from the plate. “I’m going to engineer a new method of interdimensional communication. Maybe even a means of travel to other planes of existence. This could be more powerful, more revolutionary than even the Stargate.”

He turned the broccoli in his palm, mystified, as if it were the key to the universe and time itself.

“Okay,” said Sheppard. He waited in silence, but Rodney was completely engrossed in his new discovery. “Well, if you won’t let me eat it, I’m going down to the cafeteria before lunch closes up.”

“Mhm!” Rodney lifted the multidimensional object level with his unwavering gaze, fascinated by the fact that it looked exactly like an uncooked piece of broccoli, and never noticed nor acknowledged Sheppard’s quiet exit.

#stargate atlantis #rodney mckay #john sheppard #fic prompt #my fic #physics-and-wine

7 notes · View notes

mathdevelopment · 6 years

Text

Random Math Topic of the Day: Eigenvectors

Note: Most posts on this blog focus on a programming project. This one is more about what I researched while making a programming project, linked at the end. I'm sorry if you like this kind of content less.

Welcome to #RMTotD, prounounced rm-tot'd.

So what is an eigenvector anyways? Good question. For a given transformation matrix (pretty much any square matrix, though typically we use 2x2, 3x3, and 4x4 only), there are a number of eigenvalues up to but not exceeding the size of the matrix (except for when there are infinite eigenvalues). E.g. a 2x2 matrix can have up to 2 eigenvalues, a 3x3 matrix can have up to 3 eigenvalues, a 4x4 matrix can have up to 4 eigenvalues, etc.

But what is an eigenvector, you say as I still haven't actually told you what an eigenvector is despite the fact that I implied that I would tell you.

Well, one way to understand it is that an eigenvector is a vector whose direction is the same whether or not it has been transformed. That is,

\[ \text{Let } b=Ma; \; \hat{a}=\hat{b} \]

Google says that an eigenvector is "a vector that when operated on by a given operator gives a scalar multiple of itself." That scalar is called its eigenvalue, represented by $\lambda$:

\[ Mv_{\lambda = k} = kv \]

All vectors which match the above definition are eigenvectors, and the collection of all of those vectors (hint: there's an infinite number of them for each eigenvalue. Just change k!) are called the eigenspace. Wow, sounds cool, huh? An eigenspace is easily represented by $ tv_{\lambda=k} $ (for eigenvalue $k$) but there are actually a bunch of different ways to represent an eigenspace that all pretty much mean the same thing.

"But wait!" you say frantically. "This is mathdevelopment.tumblr.com! There would never be a post on mathdevelopment.tumblr.com that didn't involve programming!"

Right you are! I produced a little site to help visualize eigenvectors for one of my former teachers to use, but I figured I would post about it here too. You'll need to sit through some more fun properties of eigenvectors before you get the juicy interactive graphs though. After all, this is mathdevelopment.tumblr.com, not randomprogrammingprojectsthatunlockeddecidedtomake.tumblr.com!

Eigenvectors have a cool property where if you have $n$ eigenvalues in an $n\text{x}n$ matrix, any point in the relevant $n$-dimensional space can be represented as a linear combination of the eigenvectors, and the transformed point will also be a combination of the initial eigenvectors multiplied by their associated eigenvalues:

\[ \text{For} \;\; v_{\lambda=a}+v_{\lambda=b}+\dotsc=v; \] \[av_{\lambda=a}+bv_{\lambda=b}+\dotsc=Mv\]

Cool.

Okay, fine, you can have the site. Click here.

#RMTotD #eigenvalue #eigenvector #eigenspace

1 note · View note

forgottenbones · 3 years

Text

mathematics is a whole lot like making up a guy to get mad about, except the guy you made up is like, an algebraic ring, or an eigenspace

— 🔪 (@leaacta) May 9, 2021

#twitter

1 note · View note

yetanothergeographer · 6 years

Photo

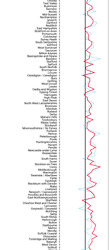
This is an interesting little exploration I did while finishing up my GISRUK data challenge analysis. It's not going into my analysis, but I like the concept, so I'll post it here (cause that's the entire point of this blog!)

I don't really have a good idea for what many places in the UK are like, nor for what the structure of some of this data is when considering its joint structure. So, while my model fits quite well and yields some interesting results, I'm a bit limited because I don't really know what a place like Barrow-in-Furness is like, without looking into it.

In general, it's more difficult to get a sense of what the model's telling me from the conditional estimates because I don't really have a sense of the joint picture: I don't really intuit how they covary across places, like I might in US counties or states.

So, I found myself wanting a kind of "joint" marginal effect, something I could use to work out how my model predictions vary from "places like A" to "places like B" but define those generically, in terms of typical combinations of attributes in my sample.

I started by shifting things linearly along my data's midranges, but this doesn't account for the fact that some attributes may be negatively correlated with other attributes in my design matrix, and so I would expect it to be more typical in my data that Xj increases as Xk decreases, on average. This isn't just a linear shifting using each conditional effect... it's something else.

So, eigenspaces. I strung some code together to:

Grab the sklearn.decomposition.PCA of my model design matrix.

Extract the most relevant dimension.

Sort my data by this dimension and grab the names of observations.

Plot the predicted Brexit % against these names.

Above is the plot of my data's main dimension, the one that explains the most variance in my design matrix. The lines are the predicted % Brexit, observed % Brexit, and "breakeven point," along with the names of places sorted by this dimension on the vertical axis.

Now, I can get a sense of how these types of places (sort of like area profiles) relate to one another in my data. This gives me an idea of what happens when I change from "places like Kensington and Chelsea" to "places like Cornwall," without having to specify the precise covariance structure of my attribute data.

I can slice one dimension off the PCA decomposition, check how varying it changes my model, and see what covariates are related to that dimension.

In a way, gives me the "joint" marginal effect I want: what happens when you move your mean response along many different features, but in a way that reflects how these features covary in your source data.

#statistics #simulation #machine learning #geography #brexit #analysis

6 notes · View notes

eigen-moved · 6 years

Photo

Some silhouette sketches for the Art War2 challenge

https://forums.cubebrush.co/t/artwar-2-2d-dechen-eigenspace/5060

#artwar2 #artwar #concept art #character design #sketch #thumbnail #silhouette

1 note · View note

irregularwebcomic · 5 years

Photo

[Irregular Webcomic! #2011 Rerun](https://ift.tt/36rVt0J)

An Eigen Plot is a story plot that is carefully designed so that every skill of every one of the protagonists, no matter how unlikely or normally useless a skill it is, is needed at some point to overcome an obstacle that would otherwise prevent the heroes from achieving their goal. There are many examples of such plots in fiction. The whole point being, of course, to make sure that each character has something important to do in the story.

The name "Eigen Plot" is taken from a set of concepts in mathematics, namely those of eigenvectors, eigenvalues, and eigenspaces.

Recall from the annotation to strip #1640 that a function is merely a thing that converts one number into another number. But actually, that's not all a function can do. You can extend this definition to say that a function is something which converts any thing into some other thing.

For example, imagine a function that converts a time into a distance. Say I walk at 100 metres per minute. Then in 3 minutes, I can walk 300 metres. To find out how far I can walk in a certain number of minutes, you apply a function that multiplies the number of minutes by 100 and converts the "minutes" to "metres".

That's a pretty simple example, and we could have done pretty much the same thing with a function that simply converts numbers by multiplying them by 100. But let's imagine now that I'm standing in a field with lots of low stone walls running in parallel from east to west. If I walk east or west, I am walking alongside the walls, and never have to climb over them. So I walk at my normal walking speed, and I still walk at 100 metres per minute. But if I walk north or south, then I have to climb over the walls to get anywhere. The result is that I can only walk at 20 metres per minute in a northerly (or southerly) direction.

So, put me in the middle of this field. Now, what function do I need to use to tell me how far I can walk in a given time? You might think that I need two different functions, one multiplying the time by 100, and another multiplying it by 20. But we can combine those into one function by making the function care about the direction of the walking. This is a perfectly good function:

If I am walking east or west, multiply the time by 100 and convert "minutes" to "metres"; if I am walking north or south, multiply the time by 20 and convert "minutes" to "metres"

What happens if I want to walk at an angle, like north-east? If the walls weren't there, I could just walk for a minute to the north-east, and end up 100 metres north-east of where I started. To figure out the equivalent in the walled field, let's break it up into walking east for a bit, and then north for a bit. On the empty field, I would need to walk east 100/sqrt(2) metres (about 71 metres), and then north 100/sqrt(2) metres. In terms of time, the equivalent of walking for 1 minute north-east is walking for 1/sqrt(2) minutes (about 42.4 seconds) east and then 1/sqrt(2) minutes north. It takes me longer (because I'm not walking the shortest distance to my destination), but the end result is the same.

But what happens if I walk for 1/sqrt(2) minutes east and then 1/sqrt(2) minutes north on the field with the walls? I end up 100/sqrt(2) metres east of where I started, but only 20/sqrt(2) metres north of where I started (because the walls slow me down as I walk north). The total distance I've walked is only a little over 72 metres, and my bearing from my starting position, rather than being north-east (or 45° north of east) is only 11.3° north of east. So the function I've described above converts a time of "1 minute north-east" into the distance "72 metres, at a bearing 11.3° north of east". An interesting function!

Here's where we come to the concept of eigenvectors. "Vector" is just a fancy mathematical name for what is essentially an arrow in a particular direction. A vector has both a length and a direction. So a vector of "1 metre north" is different from a vector of "1 metre east". And "1 metre north" is also different from a vector of "1 minute north", by the way. Okay, now we know what a vector is. What's an eigenvector?

Firstly, an eigenvector is a property of a function. Eigenvectors don't exist all by themselves - they only have meaning in the context of a particular function. That's why I went to all the bother of describing a function above. Without a function, there are no eigenvectors. Some functions have eigenvectors, and some functions don't. Okay, ready?

An eigenvector of a function is a vector that does not change direction when you apply the function to it.

An example eigenvector of our function is "1 minute east". The function changes this to "100 metres east". The direction has not changed, therefore "1 minute east" is an eigenvector of our function. Similarly, "1 minute north" is an eigenvector, because the function changes it to "20 metres north". However, "1 minute north-east" gets changed to "72 metres, at a bearing 11.3° north of east" - the direction of this vector is changed, so it is not an eigenvector of our function. In fact, vectors pointing in any direction other than exactly north, south, east, or west are changed in direction by our function, so are not eigenvectors of the function.

But the vector "2 minutes north" gets changed to "40 metres north". So "2 minutes north" is also an eigenvector of the function, just as "1 minute north" is. You've probably realised that any amount of time in the directions north, south, east, and west are also eigenvectors of the function. Our function has an infinite number of different eigenvectors.

Now we're ready to talk about eigenvalues. Again, eigenvalues are properties of a function. They don't exist without a function.

An eigenvalue of a function is the number that an eigenvector is multiplied by in order to produce the size of the vector that results when you apply the function to it.

What are the eigenvalues of our function? Well, if I walk east (or west), we need to multiply the number of minutes by 100 to get the number of metres I walk. This is true no matter how many minutes I walk. So the number 100 is an eigenvalue of the function. And if I walk north (or south), I multiply the number of minutes by 20 to get the number of metres. So the number 20 is an eigenvalue of the function.

These are the only two eigenvalues of the function: 100 and 20. I don't have to worry about vectors in any other directions, because none of those vectors are eigenvectors. And now we come to the idea of eigenspaces. Once more, eigenspaces are properties of functions.

An eigenspace of a function is the collection of eigenvectors of a function that share the same eigenvalue.

In our case, all of the eigenvectors east and west have the eigenvalue 100. So the collection of every possible number of minutes east and west forms one of the eigenspaces of the function. Similarly, all of the eigenvectors north and south share the eigenvalue 20, so make up a second eigenspace of our function. Considering the sets of eigenvectors together, the two eigenspaces of our function are a line running east-west, and a line running north-south, intersecting at my starting position.

[As an aside, let's examine briefly the walking function in a field without walls. In that case, no matter what direction I walk, I walk 100 metres per minute. "1 minute north-east" becomes "100 metres north-east". So every time vector ends up producing a distance vector in the same direction, with the number of metres equal to 100 times the number of minutes. In other words, every time vector, in every direction, is an eigenvector, with an eigenvalue of 100. This function has a lot more eigenvectors that the walled-field function, but only one eigenvalue! Which means there is only one eigenspace, but it isn't just a line in one direction, it's the whole field!]

You'll notice that the two eigenspaces of the walled-field walking function (the north-south line and the east-west line) end up aligned very neatly with the structure of the walls in the field. In general, this is true of many interesting functions in real life applications such as physics, engineering, and so on. In many fields, there are functions that describe various physical properties of things in multiple dimensions.

An example is the stretching of fabric. If you pull a fabric with a certain amount of force, it stretches by a certain amount. The amount it stretches is actually different, depending on what angle you pull at the fabric. (Anyone who does knitting or sewing will know this is the case.) You can describe this with a function that depends on the angle at which you apply the force. Once you have this function (and you could get it, for example, by actually measuring the stretching of a piece of fabric with various different forces and angles), you can calculate the eigenvectors, eigenvalues, and eigenspaces of the function. And it turns out that the eigenvectors, eigenvalues, and eigenspaces of the stretching function will be closely related to actual physical properties of the fabric, such as the directions of the weave.

A very similar case happens in three dimensions with the properties of rocks. By using seismic probing, core sampling, and other techniques, geologists can build up a three-dimensional analogue of a "stretching function" for rocks. And by calculating the eigenvectors of this function, they can figure out the directions of various features within the rocks, such as fault lines. (This is rather simplified, but that's one of the basic principles behind experimental geophysics.)

We have some loose ends to tie up. Where does the name "eigen" come from? This is actually a German word, meaning "own", in the adjectival form. So an eigenvector is an "own-vector" of a function - a vector that belongs to the function. As you can see, this is a very fitting description. The prefix "eigen" has come from this usage into (geeky) English to refer to other characteristic properties of things. One example is eigenfaces, which refers to the characteristic facial feature patterns used in various computerised facial recognition software functions.

Another example is the TV Tropes coinage of the trope Eigen Plot, which began this annotation. This is an abstracted usage, playing off the "characteristic property" implication of the "eigen" prefix. The characters in a story have a certain set of skills, so an eigen-plot is a plot that is characteristic of that set of skills (i.e. one that will exercise all of the skills).

This anotation has no relevance to today's strip, other than that Colonel Haken and Erwin are German, like the word "eigen".

2019-11-03 Rerun commentary: It's interesting that Erwin is driving the truck... but he was just out on the roof fighting with Monty, and is only shown climbing back into the truck here in panel 1. I guess Haken used his hook to steer and just jammed his left foot down on the accelerator while the fight was happening.

#Irregular Webcomic!

0 notes

thousandmaths · 7 years

Text

and it’s all just linear algebra in the end...

Hey folks, this is the last of three posts (1 2 3) based on a talk I gave yesterday, based on Steven Griffeth’s lecture series that he gave at the CRM Equivariant Combinatorics seminar.

I’m more or less using this space to write up my talk notes. Since the audience for the talk is a graduate seminar in representation theory, the post will (hopefully) be a lot more dense than the stuff I usually write here.

------

The time has come for us to start pushing toward the rational Cherednik algebra in earnest. This begins with two remarks about the theorem from before, both of which basically say that the PBW condition, which, recall, is

$$ \langle v,w \rangle_g (g(u)-u) + \langle u,v \rangle_g (g(w)-w) + \langle w,u \rangle_g (g(v)-v) = 0, $$

is a much stronger condition on the “bilinear form” than you might think.

First, suppose that $v,w\in V$ and $g\in G$ satisfy the modest condition that $\langle v,w\rangle_g \neq 0$. In this case, we can isolate the first term, divide through by the scalar, and thus see that $g(u)-u \in \text{span}\Big( g(w)-w,~ g(v)-v \Big)$. Again, this may not seem like a big deal, but look at the quantifiers: for a fixed (appropriate) choice of $v,w$ and $g$, this statement holds for all $u$!

So another way to say this is that, for any $g$ which contributes at all to the “bilinear form”, the dimension of $g-I$ is at most 2. In other words, $g$ must have a very large fixspace; and so already you’ve shown that the “bilinear form” doesn’t get any contribution from most of the group elements.

But there’s even more you can say: suppose that $v$ and $w$ are both in $\text{fix}(g)$— which, remember, is very large. Then two of the terms in the product vanish, so you just have $\langle v,w \rangle_g (g(u)-u)=0$. Now, if $g$ is not the identity, there is some $u$ which is not fixed by $g$, and hence we see that $\langle v,w\rangle_g = 0$.

So not only do most $g$ not contribute to the form, but even for those that do, there’s this huge portion of the vector space that doesn’t see its contribution.

------

If we want to understand this entire story as a sort of “$G$-equivariant” version of the Weyl algebra, we can consider $V$ to be of the form $X\oplus X^*$, and we’ll also make the restriction that any element $g\in G$ is of the form $g=g|_X + (g|_X)^*$. This is some formal requirement, but morally speaking, $G$ is supposed to be a subgroup of $\text{GL}(X)$, not just of $\text{GL}(V)$.

In this case, we can strengthen the above two remarks considerably.

For the first remark, note that if $g$ is not the identity, then it already has a nonfixed vector in $X$ and a nonfixed functional in $X^*$, so the dimension of $g-I$ is already at least $2$! So the only way for $g$ to contribute at all is if it is what we call a reflection:

$$ R = \{ r\in G: \text{codim}_X(\text{fix}(r ))=1 \}. $$

( The reason why I use this stilted language here is to emphasize that this is a little bit different from what you might have in mind: a reflection need not have order two. That’s because this is a complex dimension, so you might, say, rotate the non-fixed space by 120 degrees to get a reflection of order 3.)

The second remark tells us that $\langle v,w\rangle_r = 0$ for any $v,w\in\text{fix}(r )$, but in this setting we can also see that for any $v\in\text{fix}( r)$ and $w\in V$:

$$\langle v, w\rangle_r = \langle r^{-1}(v), w\rangle_r = \langle v, r(w) \rangle_r , $$

and therefore $\langle v, r(w)-w \rangle_r = 0$. Since $X$ has the eigenspace decomposition $X=\text{fix}(r ) \oplus\text{im}(r-I)$, and similarly for $X^*$, we now see that even if only one element of the bilinear form is in $\text{fix}(r )$, this is already enough to kill it. We conclude as follows:

Exercise. The skew-symmetric bilinear form $\langle\cdot,\cdot\rangle_r$ is defined by its action on the two-dimensional space $\text{im}(r-I)\oplus\text{im}(r^*-\text{id})$, and hence is unique up to scalars. Moreover, it has an explicit formula:

$$ \langle x,\varphi\rangle_r = \varphi(\alpha_r^\vee) \alpha_r(x), $$

for some choice of $\alpha_r\in\text{im}(r^*-\text{id})$ and $\alpha_r\in\text{im}(r-I)$.

------

We conclude with a definition.

Definition. Let $X$ be a vector space, $G\leq \text{GL}(X)$ be a finite group, and $R$ the set of reflections in $G$. For each $r\in R$, fix some $\alpha_r\in\text{im}(r^*-\text{id})$ and $\alpha_r^\vee\in\text{im}(r-I)$ such that

$$ r^*(\varphi) = \varphi - \varphi(\alpha_r^\vee)\alpha_r $$

for all $\varphi\in X^*$. Finally, let $\kappa\in\Bbb C$, and for each $r\in R$ let $c:R\to\Bbb C$ be a class function (i.e. $c_r = c_{grg^{-1}}$). Then the rational Cherednik algebra $H_{\kappa,c}(V, G)$ is the quotient of $T(V)\rtimes G$ by the ideal generated by

$xy-yx$ for all $x,y\in X$,

$\varphi\psi-\psi\varphi$ for all $\varphi,\psi\in X^*$, and

$\varphi x - x\varphi - \kappa\varphi(x) - \sum_{r\in R} c_r \varphi(\alpha_r^\vee) \alpha_r(x) r$.

This definition is mostly what you’d expect from the story above, with a couple of oddities:

In the last Exercise, we didn’t have that $r^*(\varphi)$ normalization condition. We’ve added it here so that the choice of form would be completely independent of the choice of $\alpha_r$ and $\alpha_r^\vee$. In the exercise above it was only independent up to scalar multiples, and in this definition the scalar multiple freedom is used up by the $c_r$.

[ In fact, this condition is strong enough that it completely subsumes the requirement that $\alpha_r$ and $\alpha_r^\vee$ be in the appropriate eigenspaces: we could have omitted those conditions with no effect on the definition. ]

Also, we didn’t have any conjugacy class considerations arise in this post, and yet the rational Cherednik algebra has a conjugacy class restriction on the parameter $c$. This is not actually an additional restriction: one of the statements of the Exercise from Post 2 was an equivariance condition on $\langle \cdot,\cdot\rangle_g$. If you play with the proof just a little bit, you find that

$$ (g^*(\alpha_r))(x)\varphi(g(\alpha_r^\vee))c_r = \alpha_{grg^{-1}}(x)\varphi(\alpha_{grg^{-1}}^\vee) c_{grg^{-1}}. $$

It is an easy check to see that $g^*(\alpha_r)$ and $g(\alpha_r^\vee)$ satisfy the normalization condition. Therefore we can replace them with $\alpha_{grg^{-1}}$ and $\alpha_{grg^{-1}}^\vee$ because $\alpha_s(x)\varphi(\alpha_s^\vee)$ does not depend on the choice of $\alpha_s$ and $\alpha_s^\vee$, subject to the normalization condition. Hence we see that either the $c_{r’}$ are all equal at all $r’$ conjugate to $r$, or every $\langle\cdot,\cdot\rangle_{r’}=0$ (in which case, who cares what the $c$ is...).

Finally, we have never actually specified any conditions on the bilinear form associated to the identity: $\langle\cdot,\cdot\rangle_I$. Indeed, you can trace the argument to check that there are no restrictions: whether the algebra has a PBW theorem is completely independent of this form. However, notice that for the rational Cherednik algebra we have specialized to the setting where $\langle x,\varphi\rangle_e = \varphi(x)$. The benefits of this choice are played out elsewhere in the theory, but from our perspective we can understand this as an attempt to keep it “looking like” the Weyl algebra.

[ Previous ] [ Post 3 ]

4 notes · View notes

mathematicianadda · 4 years

Text

Proof a 'well-known' result of Shimura on periods of modular forms https://ift.tt/eA8V8J

It is often noted in the literature that there are certain complex periods that allow one to normalize the modular symbol associated to a modular form in such a way that its coefficients are algebraic. This process of normalization by complex periods is regularly attributed to Shimura, though I can't seem to find a concrete reference explaining this result.

More precisely, let $ \Gamma=\Gamma_0(N)$ and fix an eigenform $f\in S_k(\Gamma)$. The modular symbol $\xi_f\in \operatorname{Hom}_{\Gamma}(\operatorname{Div}^0(\mathbb{P}^1(\mathbb{Q})),V_{k-2}(\mathbb{C}))$, where $V_{k-2}(\mathbb{C})$ is the space of homogeneous polynomials with complex coefficients of degree $k-2$, attached to $f$ is defined by $$ \xi_f(\{r\}-\{s\})=2\pi i \int_s^r f(z)(zX+Y)^{k-2}dz. $$ One can expand this into a homogeneous polynomial $\sum_{j=0}^{k-2} c_jX^jY^{k-2-j}$ where $c_j=\binom{k-2}{j}2\pi i \int_s^rf(z)z^jdz$. The matrix $\begin{pmatrix} -1 &0\\ 0&1\end{pmatrix}$ normalizes $\Gamma$, so the modular symbols come equipped with an involution, and hence there is a unique eigenspace decomposition $\xi_f=\xi_f^++\xi_f^-$, with $\xi^\pm$ in the $\pm 1$-eigenspace.

The follow theorem is stated in the literature (see, for example, [Greenberg-Stevens, 3.5.4], [Bertolini-Darmon,1.1], or [Pollack-Weston,page 7]).

Theorem. There exists complex numbers $\Omega_f^\pm$ such that $\xi_f^\pm/\Omega_f^\pm$ takes values in $V_{k-2}(K_f)$, where $K_f$ is the number field generated by the Fourier coefficients of $f$.

Greenberg-Stevens cite this 1977 paper of Shimura, Pollack-Weston cite Shimura's book on automorphic functions, and the Bertolini-Darmon does not give a reference. I could not find anything helpful in Shimura's automorphic function book, but I think theorem 1 from the 1977 paper is probably what we want. For simplicity, we state it below in the case where $f$ has rational coefficients.

Theorem. (Shimura, Theorem 1) Fix a primitive Dirichlet character $\chi$. There exist complex numbers $u_f^\pm$ such that $$ \frac{L(f_\chi,j)}{u_f^\epsilon\tau(\chi)(2\pi i)^j}\in K_fK_\chi $$ where $0< j< k$, $\epsilon$ is the sign of $\chi(-1)(-1)^j$, $\tau(\chi)$ is the classical Gauss sum, and $L(f_\chi,s)=\sum\chi(n)a_nn^{-s}$ is the $L$-function of $f$ twisted by $\chi$.

In fact, Shimura gives precise (though rather noncanonical) descriptions of these periods $u_f^\pm$: they are essentially the value of the $L$-function at $k-1$.

I would like to know how the first theorem stated above follows from this theorem 1 of Shimura.

It seems like a nontrivial exercise, or perhaps I am just having some trouble connecting the dots. I would also be content to see a reference which outlines a proof of the first theorem above.

My thoughts are roughly the following. With the notation as above, let $m$ be the conductor of $\chi$. I know that (see [Mazur-Tate-Teitelbaum, 8.6], for example) one has the following connection between coefficients of the modular symbols and special values of $L$-functions $$ \frac{j!}{(-2\pi i)^{j+1}}\frac{m^{j+1}}{\tau(\bar \chi)}L(f_{\bar\chi},j+1) =\sum_{a\in (\mathbb{Z}/m\mathbb{Z})^\times}\chi(a)\int_{-a/m}^{i\infty} f(z)z^j dz, $$ for $0\leq j \leq k-2$. This tells us, for example, that certain weighted sums of the coefficients of $\xi_f(\{\infty\}-\{a/m\})$ can be scaled to be algebraic. Even more, after writing down the symbols $\xi_f^\pm$, I can find periods $\Omega_f^\pm$ such that, roughly speaking, $$ \frac{1}{\Omega_f^\pm}\sum\chi(a)(\text{$j$th coefficient of $\xi_f^\pm(\{\infty\}-\{a/m\}$}) ) $$ is algebraic, but again, this only tells me that (a) certain weighted sums of the coefficients are algebraic, and (b) only gives information about the modular symbol evaluated at $\{\infty\}-\{a/m\}$, which as far as I can tell, is not the generality needed for the first theorem above.

from Hot Weekly Questions - Mathematics Stack Exchange Arbutus from Blogger https://ift.tt/32VNcD4

#Blogger

0 notes