#What Ramanujan invented

[krystaln78]

HOW TO COMMUNICATE WITH THE UNIVERSE

I won’t lie. I’m exactly the kind of girl who likes scrolling on Instagram reels. But I don’t watch those reels where this nation’s youth is immersed in following useless trends. Not the reels with exaggerated faces, dances with zero elegance and charm, and dham dham music. I don’t have an account of my own. 

The algorithm usually recommends me videos of poetry, food or school. In fact, that is how I found my favourite poet Mahmoud Darwish. He was of Palestinian descent, and was declared as Palestine’s national poet. I read the English translations of his Arabic poetry(see, Instagram has some purpose). 

But, that is not the point. The point is, when I was keeping myself busy by participating in my daily ritual of scrolling on Instagram(all while releasing an unhealthy amount of dopamine because that’s what a high school student lacks the most), I found a video which said that Mathematics was the language that we(as in, the human race)used to communicate with the universe. 

And I do not say this out of my frustration with the Math subject, but that statement is so so false. Sure, Mathematics is a type of language. It’s a type of language which we ourselves don’t know whether it has been invented or discovered. However, we cannot communicate with the ethereal beauty of the universe, its stars, galaxies and planets, with representations of numbers. (For example, fractions. Nobody says they ate 2/4th of a pizza. They say they ate two slices of a pizza. And nobody wants to add the numbers either. They only want to add more pizzas.) The logics and statistics and proofs that the human race has achieved in the field of Mathematics is incredible(lookin’ at you, Srinivas Ramanujan and Aryabhatta)but we cannot use it to communicate with the universe. 

Rather, I would say that Mathematics is the language that is used to understand the universe. The way we communicate with the universe is different for every individual. To communicate with it, one must have ambition and resource to embark on a journey of understanding. Some people have already realised this and started this journey, these people, we term as ‘spiritual’. Common people like, for example, Mahmoud Darwish communicate with the universe with their words. People like M.F. Hussain communicate with their artworks. With colours, shades and hues. Now, I don’t know any famous music players so I can’t take any name, but, musically gifted people communicate with the universe with their outstanding melody that charms the ears. 

The funny thing is, there’s this thing called Artificial Intelligence(AI) which can replace all poetry, art and music. In an instant. With a click of your keyboard. With a jerk of your fingertips. Let Sam Altman being fired be a lesson. AI has the ability to do more harm than good. Haven’t we watched enough movies? We are destroying our Earth, let us not cut off our only way of communication with life, light and darkness beyond the exosphere. 

My point is not to order you to stop using AI or limit your uses of AI. But think before you do. Do you really need AI to write an essay that you could write? Do you really need it to impersonate the human ability of musical charm? Then, what is our identity as a species? Buffoons who manipulated technology to impersonate them?

#teen poetry #young poets #indian poets #teenagers #universe #communication #divine #humans #talent #nature #powerful #meaning #existence #meaning of life #spiritual disciplines

[falseandrealultravival]

Is a two-digit multiplication table necessary?: Mathematics Note- 4 (essay)

In some countries, such as India, elementary school students are taught two-digit multiplication tables. If it's a single-digit multiplication table, you have to memorize 9*9=81 ways, but if you have two digits, you have to remember 99*99=9801 ways. It takes 121 times more effort. I wish I could put that effort into something else. Multiplication can be done by memorizing single-digit multiplication tables. I don't think it's necessary to memorize two-digit multiplication tables.

The great mathematician Gauss was so good at calculations that he could memorize two-digit multiplication tables, but for complex calculations, he used a man with a unique talent for calculations. Today, we are more fortunate than Gauss because we have the convenience of a calculator. I think the problem is not how much computing power you have, but how you can set the problem. In an era where calculation itself can be left to computers, I think what is required is the ability to set problems.

Speaking of India, Masahiko Fujiwara, a professor at Ochanomizu University, took up an Indian mathematician named Ramanujan in his book "The Glory and Frustration of a Genius." Ramanujan had an outstanding ability to create "formulas," but he did not understand the meaning of "proofs," and it is said that British mathematicians Littlewood and Hardy (both professors at Cambridge University) worked hard to come up with proofs. . He said, "Goddess gives it to me," and the subtleties of his ideas, but I cannot say that Ramanujan is a first-rate mathematician. What he did was "invent a calculation formula". He mass-produced useful tools, so to speak. However, the tool is not a large tool such as differentiation and integration, but a small tool.

What Ramanujan did was "calculation". Galois of France, who was also featured in ``The Glory and Frustration of Genius'', questioned ``the meaning of calculation'' through his ``group theory''. This makes the qualitative difference between the two performances huge. The essence of mathematics lies not only in the tools, but in the mastery of them, and even more not in the mastery of them, but in knowing the limits of their application.

#two-digit multiplication table #Gauss #Ramanujan #formula #proof #Cambridge University #Galois #group theory #mathematics #essay

[muruganmumbai]

Ready for 1,2,3...? 1st.... Have we found OUR PASSION....? Nightingale had a passion for treating patients...! Wright brothers...? Flying was their passion...! Edmund hillary & norgay ...? climbing mountains...! Srinivasa Ramanujan....? Solving maths...! Einstein...? Inventing new things...! What ignites.... our mind, body & soul, is our passion...! 2nd.. find out the purpose of our life & this wonderful 👍 journey....! we are in this marvelous journey... What for...,? Just to make money...? Just to live a very ordinary life....? & When we find out the purpose of our life, that's the day, we understand meaning of life...! Now ... Miracles....! unbelievable things happen, When you connect your passion & Purpose...! I hope & believe, Wonderful things are happening, & will continue to happen...! I Mumbai Murugan.... https://www.instagram.com/p/CiDSkGFpihp/?igshid=NGJjMDIxMWI=

[mahanok]

about Srinivasa Ramanujan You should know about these 10 facts

केवल 32 साल की उम्र के भारतीय गणितज्ञ Srinivasa Ramanujan ने गणित में संख्या सिद्धांत में क्षेत्र में कई अद्भुत आविष्कार किए। श्रीनिवास रामानुजन के बारे में और उनके जीवन के बारे में जानेंगे इस about Srinivasa Ramanujan history ब्लॉग से और biography के रूप में से समझेंगे। 

  about Srinivasa Ramanujan short biography           about Srinivasa Ramanujan

  Barth death                      >      22…

View On WordPress

#about ramanujan #about srinivasa ramanujan #biography of ramanujan #ramanujan birthday #ramanujan photo #Srinivasa Ramanujan achievements #Srinivasa Ramanujan biography #srinivasa ramanujan death #srinivasa ramanujan education #srinivasa ramanujan history #srinivasa ramanujan movie #Srinivasa Ramanujan number #srinivasa ramanujan short biography #stories in hindi #What Ramanujan invented #Why is 1729 a special number?

[sciencespies]

Scientists invent a machine that generates mathematics we've never seen before

https://sciencespies.com/physics/scientists-invent-a-machine-that-generates-mathematics-weve-never-seen-before/

Scientists invent a machine that generates mathematics we've never seen before

His name was Srinivasa Ramanujan, and he had a unique gift for dreaming up mathematics of a kind few, if any, had ever contemplated.

Attributing his skills to a divine goddess, the Indian mathematician introduced thousands of mathematical ideas and equations to the world, and was especially known for devising conjectures: mathematical propositions not yet proven to be true (in which case they become classified as theorems).

Such an ability – crafting mathematical statements that are both informed and yet uncertain – is rare, and relatively few mathematicians make their name on the basis of such output, let alone theorists with little in the way of formal training.

But now, a new algorithmic invention developed by researchers in Israel could help us automate the discovery of mathematical conjectures like those Ramanujan once pioneered.

Named after Ramanujan – who died in India at the age of 32 – the ‘Ramanujan Machine’ is a computerised system capable of self-generating conjectures involving mathematical constants: strange numbers like π and e that seem to crop up all over the place, even if entirely by coincidence.

“Fundamental mathematical constants such as e and π are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry,” researchers from Technion – Israel Institute of Technology explain in a newly published study detailing the system.

“Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically.”

The Ramanujan Machine might speed things up a little on that front. A system of algorithms powered by a community of cloud-connected computers, it’s capable of producing conjectures and discovering mathematical formulas for fundamental constants that stand to reveal the underlying structure of the constants.

So far, the algorithmic machine has generated conjectures that were easily provable, while discovering new fractional ways to calculate constants like π, and also coming up with conjectures that are yet to be proven.

“The computer doesn’t care if proving the formula is easy or difficult, and doesn’t base the new results on any prior mathematical knowledge, but only on the numbers in mathematical constants,” explains senior author and physicist Ido Kaminer.

“It’s important to point out that the algorithm itself is incapable of proving the conjectures it found – at this point, the task is left to be resolved by human mathematicians.”

The researchers observe there are limitations to what the Ramanujan Machine can produce; notably, in some instances, what appear to be previously unknown conjectures generated by the algorithms may be “merely mathematical coincidences that break down once enough digits are calculated”.

So far, however, there are reasons to get excited about what these algorithms are enabling – especially the discovery of a new algebraic structure concealed within Catalan’s constant, which hints the machine might be capable of generating actual breakthroughs the math world has never seen before.

“We believe and hope that proofs of new computer-generated conjectures on fundamental constants will help to create mathematical knowledge,” the researchers explain.

If you like the idea and want to get involved, there are several perks to unlock if you join the Ramanujan Machine’s community. Lend your computer’s processing power, and you might get a conjecture named after you.

Formulas and algorithms themselves are also up for naming rights, depending on your aptitude for mathematical proofs or developing code.

The findings are reported in Nature.

#Physics

#02-2021 Science News #2021 Science News #Earth Environment #earth science #Environment and Nature #Nature Science #News Science Spies #Our Nature #outrageous acts of science #planetary science #Science #Science Channel #science documentary #Science News #Science Spies #Science Spies News #Space Physics & Nature #Space Science #Physics

[tomasorban]

THE DREAMING SELF: HOW MUCH DO WE REALLY KNOW ABOUT DREAMS?

Time has revealed dream phenomena as paradoxical realms that are highly resistant to empirical investigation. Despite attempts to probe, encroach upon, uncover, and map territory traditionally exalted under philosophical inquiry, they remain enigmatic and ineffable.

           Dreams fascinate, mesmerize us, and pique our curiosity, namely because they appear so diametrically opposed to waking conscious experience in terms of both form and content. They violate Aristotelian homogeneity without shame. In fact, the hallmark mental characteristics of dreams–the dearth of metacognition, severe disorientation, amnesia, confabulation, misperception, reflexive recourse to hyper-associations, and the loss of an analytical anchor–more closely resemble episodes of psychotic decompensation than anything we might experience in self-regulated conscious states.

Well, what happens in a cinematic and surrealistic dreamscape is that… our gelatinous legs won’t carry us to safety after our brains issue the motor command; we see no issue with giving a public speech whilst concurrently disrobing; we strangle strangers in our rage on impulse without remorse or fear of punishment; and our best beloved transmute into theriomorphs and then reassume human form–and there’s nothing at all anomalous about that. Sometimes the Eiffel Tower is in our backyard, and sometimes we instinctively know who somebody is despite their deceptive Protean disguise. It’s all arbitrary, nonsensical, and paradoxical, at least when equated with the self-referential processes of diurnal arousal, yet it all makes perfect sense when subjectively appraised from within the perceptual context it occurred.

Examining the phenomenon from a sociohistorical perspective, one cannot deny the eminence and exalted position dreams held in antiquity. During the Greco-Roman period individuals with an ailment might pilgrimage to the temple of the god Asclepius where they would slumber in the abaton, hoping that explicit details of a cure might be revealed to them in an extraordinary dream.  A protracted period of intellectual somnolence ensued during the Middle Ages, the Renaissance, and the Age of Enlightenment, however interest in the topic was reignited with the publication of Freud’s seminal work on the topic, The Interpretation of Dreams (1899). While his theories of dreams as an unconscious embodiment of wish fulfilment may not be as empirically veracious as he would have liked, Freud was instrumental in broaching the topic as a mental phenomenon worthy of philosophical consideration and scientific exploration. Jung began where Freud tapered off, interpreting dreams as a vehicle for the expression of archetypal raw material irrupting from the collective unconscious. The imbuing of dreams with meaning had a snowball effect, and more and more thinkers were now joining the coterie eager to unlock their deepest and most profound mysteries. As one might expect, the philosophical interest in causality generated an emerging counterculture as well with Harvard University psychiatrists like Hobson and McCarley opting for a more reductive physiological approach which presupposes that the brain is a “dream-state generator” and dreams random byproducts of nocturnal brain activation.

           Founded on logical operative cognition, the operative neuroscientific tools of today–PET scans, MRIs, and EEGs–have been inept at capturing the phenomenal essence of dreams. Subjective self-report is the only known window into dream phenomenology, and this is bound to stir at the very least discomfort and at most feelings of anathema in those with dogmatic adherence to the assumptive worldview of eliminative materialism.

How does one render the dream amenable to objective measurement when people struggle to recollect explicit details after waking? This, in fact, is a very valid question. Scientists will argue that subjective accounts are mutable and empirically unreliable–if we can’t reach a unanimous appraisal on a consensual public mugging, then what hope is there of giving a veracious account of a nebulous dream narrative unfolding at a time when memory processes are in complete abeyance? Here lies the conundrum…

           Despite the gaping conceptual chasm, there is some agreement amongst cognitive scientists regarding the interpretative nature of physiological investigations. Animal studies with maze-running rats, for instance, have shown that the prima materia of the dream is real-life experience. Dreamscapes are jumbled, reassembled, and reordered waking experiences–a nonphysical dimension and perceptual space where past templates are utilized as predictive devices to determine how future events might unravel. Neuroimaging studies generally show increased activation in mesial temporal lobe and prefrontal lobe structures during dream states, and hence corroborate this conjecture. Dreams are purportedly salubrious, exerting a positive influence on mood and a regulatory effect on the body’s biochemical and immunological functions. This much we do know.

           In hindsight, we see that there are purely psychological and more physiological-evolutionary explanations able to theoretically couch and account for dreaming cognition. Which of the two should we preference, if any? Or should we try to circumvent the impediment of an internalized either-or philosophy predicated on the Kantian-Cartesian epistemological box and take a more integrative approach to dreaming cognition?

           Recently I encountered an article by Graveline and Wamsley (2015) entitled Dreaming and Waking Cognition. In it the authors make a decisive argument against higher order interpretations which tend to imbue dream imagery with symbolism and allegorical meaning. Moreover, they scrutinize the interpretability of dreams in clinical settings. While I do not detest nor repudiate the idea of dreaming and waking cognition as commensurable phenomena with shared neurobiological and phenomenological correlates, I do wonder about their appraisal and treatment of an altered conscious state, one that lies on the furthest boundaries of the human consciousness spectrum, as if it were a homogenous and monolithic neurophenomenological entity.

If waking conscious awareness can manifest with variabilities in form and content (i.e., relaxed state, hypnoid state, hypoarousal, psychosis, delirium, coma), then there’s reason to believe that the same heterogeneity also exists in dreaming states. “Shared” correlates implies latitude for phenomenal variability and anomaly; nothing is absolute. The underlying unconscious assumption of a binary system with discrete functional units is an intellectual trap in consciousness research, one which we should avoiding making at all costs.

In and of themselves theories must remain unbiased and accommodate all observed and reported data, not just the preferred data sets. Currently, the hegemony of the Western mind sciences does not permit conceptualizations of the nonphysical mind as distinct from the brain, a phenomenon which has precipitated the dismissal of precognitive dreams as a respectable domain of scientific investigation. Historiographical accounts of polymaths, scientists, and creative luminaries converge on the dream as an illumination phase of the creative process. Emerging as instances of historical novelty, profound scientific discoveries and truths which initiate radical shifts from conventional dominant paradigms or shatter them altogether are frequently epiphenomena of dream states.

Kekule came up with a simple structure for benzene after experiencing a hypnogogic vision in which carbon atoms congregated in the form of an ouroboros, a snake biting its own tail. The celebrated Indian mathematician Srinivasan Ramanujan claimed the Hindi goddess revealed mathematical formulas, equations, and conjectures to him in the dream state. For Rene Descartes, a series of dreams served as inspiration for the development of the scientific method. How these profound illuminations occur in an input-deprived cortex starved of logical operative cognition eludes understanding and cannot be feasibly explained by any existing neurophenomenological model of the human mind and consciousness.

Indeed, scientific progress in this field may be illusory and may continue to be under the auspices of the reductionistic agenda. As the philosopher Colin McGinn eloquently asserts, humans suffer from “cognitive closure” and have invented scientific tools that are essentially products of logical operative cognition; they cannot detect, let alone investigate, quintessential nonphysical phenomena on the other side of that boundary. In the final analysis, we may have reached a stalemate when it comes to our spirited investigation of dreams, one likely to persist until there is a radical shift in the ontological and epistemological axis of science.

#consciousness #psychology #philosophy #science #mind

[lickrock]

You see an infinite amount of posts about Tesla on this website, but not once have I found a post about his visions.

At one point of his life he felt he was going medically insane. But later on in life he came to accept them and the vast mayority of his inventions came to him firstly in either the form of visions or night dreams, almost in the same fashion as Srinivasa Ramanujan’s dreams, who, in a matter of two years solved mathematical problems that were thought to be humanly impossible to solve.

When Ramanujan was asked by Cambridge professors about how he came to his methods, he answered he saw the answers in his dreams, or that sometimes a woman would whisper the answers in his ear while he was falling asleep. He was not trained in pure mathematics, so he had no way to prove that the solutions coming from his dreams were valid. He eventually trained himself in pure mathematics to prove that his solutions were correct. And he accomplished it. Even the theorems that were not understood back then are being proved to be accurate nowadays. The mathematical functions he wrote in his deathbed in 1920 are currently believed to shed some light about the behavior of blackholes.

When Tesla was asked about his Alternating Current invention, he said he saw it vividly right infront of him. No theorical analysis and no drafting. He could just see the whole mechanism working right in front of him as if it was real. He saw the electric transmission of information and images in his dreams. “When wireless is perfectly applied the whole earth will be converted into a huge brain, which in fact it is, all things being particles of a real and rhythmic whole. We shall be able to communicate with one another instantly, irrespective of distance. Not only this, but through television and telephony we shall see and hear one another as perfectly as though we were face to face, despite intervening distances of thousands of miles; and the instruments through which we shall be able to do his will be amazingly simple compared with our present telephone. A man will be able to carry one in his vest pocket.”

I mean, you can take this tendency for imaginative creativeness as pure intuition, which completely resonates to their thinking process. But both men themselves were convinced there was more than intuition involved in their creations. They were aware they didn’t fully understand what was happening inside their mind, but they worked their ass off to prove what they saw was real. And if this isn’t terrifying, I don’t know what is.

#seriously though #when you read the personal notes of both Tesla and Ramanujan it’s scary to see how similar their tendency to visions and dreams was #and everything they solved or created came to them in these visions #another creepy example of this was Carl Jung’s and Tolkien’s similarities in visions and dreams even though they never met each other #Carl Jung had imaginative dreams about lands similar to Tolkien’s LOTR #they both even painted their visions simultaneaously and they both painted the eye #Tolkien explained many times too that he created the elfish language cause he heard it in his dreams #so yep #creepy #Nikola Tesla #Srinivasa Ramanujan

[startupupdates]

Ramanujan - The Indian genius who changed the world of mathematics

New Post has been published on https://startupupdates.info/ramanujan-the-indian-genius-who-changed-the-world-of-mathematics/

Ramanujan - The Indian genius who changed the world of mathematics

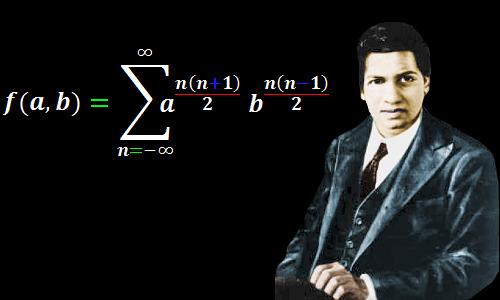
 In an interview by Paul Erdős, when Hardy was asked what his greatest contribution to mathematics was, Hardy unhesitatingly replied that it was the discovery of Ramanujan. So think how genius Ramanujan was , When one of greatest mathematician of 20th century unhesitatingly replied that his greatest contribution was not any mathematics discovery but discovery of one Indian genius.

Introduction

Srinivasa Ramanujan was born on December 22, 1887 and was predetermined to gotten to be a brilliant mathematician. Over the course of his life, he went on to create thousands of his own formulas, numerous of which have kept on be utilized in mathematics and science. In fact his Formula are indeed utilized to understand  dark holes. He initially made a few of his theories while in India , in spite of the fact that when he travelled to Cambridge in Britain to talk about his scientific equations with the brightest minds of the time, he made numerous there as well. It was in Britain that Ramanujan started  an inspirational partnership with the Cambridge teacher Godfrey Harold Hardy. Professor Hardy  figured it out that Ramanujan had found certain mathematical formulas by himself that were really as of now known to the mathematical elite. However, what was more striking was that he created his own formulas, which warranted further understanding. Most of his theories have been proven correct over time and have provided mathematicians since then with the basis from which to create formulas that continue to shape science today.

Early Life

Srinivasa Ramanujan was born in Erode, a city which is  presently in the Indian state of Tamil Nadu. His father, K. Srinivasa Iyengar, was a receptionist in a sari shop whereas his mother, Komalatammal, was a housewife who frequently sang religious hymns at the local Hindu temple. When he was just two years old, Ramanujan contracted smallpox and later recovered from the disease. As a child, he did not like attending school and his family even enlisted the help of a local constable to ensure that he actually attended. Paradoxically, it was at Kangayan Primary School that he really flourished. He performed very well academically. In November 1897, at nine years old, Ramanujan completed his primary school education and scored the highest marks in his local district. He then enrolled at Town Higher Secondary School. It was there that his love and fascination with mathematics began.

Ramanujan’s thirst for mathematical knowledge was unquenchable. By the age of 13, he had mastered a textbook by Professor Sidney Luxton Loney on advanced trigonometry, or the study of relationships involving the lengths and angles of triangles. Within a couple of years he was discovering complex mathematical theories on his own, creating his own formulas and even completed mathematical examinations in less than half the allocated time.

Ramanujan received a copy of A Synopsis of Elementary Results in Pure and Applied Mathematics by the mathematician George Shoobridge Carr from a friend. This contained a staggering 5,000 of Carr’s own theories. It is generally believed that by studying this book Ramanujan’s mathematical prowess was awakened. In 1904, he was awarded the K. Ranganatha Rao prize by his school’s headmaster, after which he received a scholarship at Government Arts College in Kumbakonam. While there he was so enamoured with mathematics that he neglected all other subjects, and subsequently lost his scholarship. Ramanujan would later enroll at Pachaiyappa’s College in Madras, now known as Chennai. He failed in his Fellow of Arts degree as he again did not perform well in subjects other than mathematics. He sat for the examinations again a year later but also failed. Since he lacked a degree, he left formal education to pursue his work independently and because he lacked formal qualifications, he concentrated on his theories alone, living in utter poverty and was often on the brink of starvation.

Adulthood

In 1909, at the age of 22, Ramanujan was married to Srimathi Janaki, also known as Janakiammal. At this time in history, it was not unusual for marriages to be arranged with girls who were much younger than the husband. This was the case for Ramanujan’s marriage to Srimathi Janaki who was only 10 years old at the time.

Following this, Ramanujan spent time looking for work in Chennai, while living in his friend’s house. At the same time, to earn some money, he gave tuition to students from Presidency College, one of the oldest government arts colleges in India and one of the two Presidency colleges established by the British. At that time the Indian Mathematical Society of India was formed by V. Ramaswamy Aiyer, whom Ramanujan met with when he was looking for a job. Later, Aiyer recalled looking through Ramanujan’s notebooks upon meeting him.

“I was struck by the extraordinary mathematical results contained in it [the notebooks]. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.”

This meeting was to be fortunate for Ramanujan, as he was soon sent to Chennai with letters of introduction from Aiyer. There he met with Aiyer’s mathematical peers, who again gave him letters of introduction and sent him to Raghunatha Ramachandra Rao, an Indian civil servant, mathematician and social and political activist and the secretary of the Indian Mathematical Society. Upon first meeting Ramanujan, Rao was unconvinced regarding his mathematical formulas and thought him a fraud. However upon talking and discussing various complicated mathematical theories with Ramanujan, he was won over by the young man’s mathematical genius. Ramanujan requested Rao’s help for financial aid while he continued his research and Rao happily obliged. This eventually led to Ramanujan having his work published in the Journal of the Indian Mathematical Society.

In 1912, Ramanujan applied for a temporary job in the Madras Accountant General’s office. There he was supposed to earn 20 Indian rupees a month, but he was only in this position for a couple of weeks. During this time, he applied for a job under the Chief Accountant of the Madras Port Trust. His application was accompanied by a letter of recommendation from Edgar William Middlemast, a professor of mathematics at Presidency College. This application landed Ramanujan a job as a Class III, Grade IV accounting clerk on March 1, 1912 with a monthly salary of 30 rupees. Ramanujan was adept at the work, finishing his assignments quickly, allowing him ample time to continue his research. His boss, Sir Francis Spring and his colleague, S. Narayana Iyer encouraged Ramanujan in his research.

In 1913, Diwan Bahadur Rao, Professor Middlemast and S. Narayana Iyer attempted to present Ramanujan’s work to various British mathematicians. Many of them ridiculed Ramanujan’s work, labelling him uneducated and a fraud. It was then that Ramanujan wrote to the mathematical elite at Cambridge University in England. Though he received the same negative reception from two professors, he received a warmer response from Professor Godfrey Harold Hardy. Though initially sceptical of Ramanujan’s work, upon analysing his manuscript further he was very impressed with some of his theories. Professor Hardy even stated that Ramanujan’s theories.

“defeated me completely; I had never seen anything in the least like them before”

and that his theories

“must be true, because, if they were not true, no one would have the imagination to invent them.”

After conferring with his colleague, Professor John Edensor Littlewood, who was equally impressed with Ramanujan’s work, Professor Hardy described him as a mathematician of the highest quality, a man whose work was original and powerful.

Professor Hardy wrote back to Ramanujan asking for more proof of his theories and began to arrange for Ramanujan to travel to Cambridge, contacting the Indian Office. Secretary Arthur Davies from the Advisory Committee for Indian Studies met with Ramanujan to discuss his trip to England, but Ramanujan refused to travel overseas to a foreign land, in observance of his strict Brahmin (priestly-caste) upbringing.

Despite this, Ramanujan felt very fortunate to have found such a friend. Professor Hardy even arranged, through his peers, for Ramanujan to receive a two-year research scholarship of 75 rupees a month from the University of Madras. While there he continued to submit papers containing his theories to the Journal of the Indian Mathematical Society.

There was a notable instance during which Ramanujan had pre-empted the work of another mathematician. Professor Edward Ross of Madras Christian College, who Ramanujan had met before, stormed into class one day. Flustered, he asked his students if Ramanujan knew Polish. It turned out that Ramanujan had written theories pre-empting the work of a Polish mathematician that had just arrived in the day’s mail.

Though dismayed at Ramanujan’s refusal to travel to Cambridge, Professor Hardy did not give up and enlisted the help of his colleague E. H. Neville. Over time, when Neville questioned Ramanujan regarding his refusal, it turned out that he no longer held reservations about traveling. Ramanujan promptly left for England, leaving his parents and wife behind in India.

Traveling to England and Life in Cambridge

Ramanujan’s journey from India to England took almost a whole month by sea. Traveling from Madras on March 17, 1914, he arrived in the ports of London on April 14. When he arrived, Ramanujan was whisked away to Cambridge after a couple of days stay in London. In Cambridge, Ramanujan was housed a short distance away from Professor Hardy’s own room. There he began working with Professor Hardy and Professor Littlewood almost immediately.

Studying his notebooks, they found many theories. Some had already been discovered by other mathematicians of the past, some they concluded were wrong and others they decided were complete breakthroughs. They were absolutely stunned by his brilliance, even comparing him to two of history’s most well-known mathematicians – Leonhard Euler and Carl Gustav Jacob Jacobi. Throughout Ramanujan’s time in England, Professor Hardy tried to provide Ramanujan with an education in the areas that he was not familiar with.

His five years spent in Cambridge was not without its difficulties. There was a clash of cultures between Ramanujan who came from a traditional Indian background and the two Cambridge professors. They had differences not only in the ways they worked together, but also in their beliefs. Ramanujan was a devout Hindu who relied on his intuition, whereas his colleague Professor Hardy was a stout atheist who only believed in what could be proven and in mathematics.

In March 1916, Ramanujan was awarded a PhD (then known as a Bachelor of Science) degree for his mathematical work, part of which was published as an academic paper in the journal Proceedings of the London Mathematical Society. This began a period of acceptance for Ramanujan and his work. He was elected to the London Mathematical Society in 1917, and then as Fellow of the Royal Society in 1918, the oldest scientific academy that still exists. He was only 31 years old at the time, making him one of the youngest Fellows since the Royal Society began in 1660. This award is only granted to those who have made a ‘substantial contribution to the improvement of natural knowledge, including mathematics, engineering science and medical science’. Other notable Fellows of the Royal Society include the likes of Sir Isaac Newton, Charles Darwin, Michael Faraday, Albert Einstein and Alan Turing. In 1918, Ramanuja made history by becoming the first ever Indian to be elected a Fellow of Trinity College, Cambridge.

Divine Mathematics

Ramanujan was born into a deeply religious Hindu family. Since his father spent most of the day at work, he was especially close to his mother. It was from her that he learned of the ancient Hindu tradition, learned to sing religious hymns, was encouraged to attend religious services at the local temples and learned the ways of the Brahmin (priestly) caste.

Ramanujan’s original refusal of Professor Hardy’s invitation to travel to England came about from his strict orthodox Hindu lifestyle, which prohibited him from travelling overseas. His parents also objected to this invitation, in accordance with their Brahmin upbringing.

However, his mother’s opposition was withdrawn after she received a dream from the family goddess, Namagiri, who told her not to stand in the way of her son and the fulfilment of his life’s purpose. Once he received her permission he promptly embarked on his journey that would bring him acclaim and establish his works among those of the world’s leading mathematical elite.

Following his deeply held beliefs, Ramanujan actually attributed his mathematical genius to this very same goddess, Namagiri. In fact he is known to have said,

“an equation for me has no meaning, unless it expresses a thought of God.”

Death and Acknowledgment

Ramanujan was never a very healthy person and suffered from illness and health issues throughout his life. This was exacerbated while in England, since he was not used to the foreign environment. He spent time at a sanatorium, or hospital for long-term illness after he was diagnosed with tuberculosis and a severe vitamin deficiency. Following this, he returned to India in 1919 but sadly, he passed away just a year later in 1920. He was 32 years old at the time of his passing. Ramanujan was survived by his wife Srimathi Janaki. Following an examination of his medical records, some experts have argued that his tuberculosis diagnosis was mistaken. They claim that he actually suffered from hepatic amoebiasis, a disease that could have been treated and even cured at the time.

Given his legacy as a great mathematician whose formulas still form the basis of many advanced equations and theories, his life and work have been celebrated in many ways. In 1962, the 75th anniversary of his birth, the Government of India released a memorial postal stamp in remembrance of his life and deeds. A new design of the stamp was released in 2011.

Learning institutions such as Government Arts College in Kumbakonam and IIT Madras in Chennai celebrate his achievements annually on what is referred to as Ramanujan Day. Various prizes for young mathematicians have also been started in his name, for example by the International Centre for Theoretical Physics, the SASTRA University and the Vasavi College of Engineering.

On December 22, 2011, the 125th anniversary of his birth, the Government of India declared that December 22 would be celebrated as ‘National Mathematics Day’ every year in honour of Srinivasa Ramanujan.

[mathematicianadda]

What is the Ramanujan summation for the series $\sqrt[n]{2}$ https://ift.tt/eA8V8J

A Ramanujan summation is a

technique invented by the mathematician Srinivasa Ramanujan for assigning a value to divergent infinite series

In my case, I'm interested in assigning a value to the divergent series

$$\sum_{n=1}^\infty f(n) \ \ \ \ \ \ \ \text{where}\ \ \ \ f(n)=\sqrt[n]{2}$$

According to the Wikipedia page (and my understanding), the Ramanujan summation is

$$\sum_{n=1}^\mathfrak{R} f(n)=\lim_{N\to\infty}\Bigg[\sum_{n=1}^N f(n)-\int_{1}^N f(t)dt\Bigg]$$

Thus

$$\sum_{n=1}^\mathfrak{R} \sqrt[n]{2}=\lim_{N\to\infty}\Bigg[\sum_{n=1}^N \sqrt[n]{2}-\int_{1}^N \sqrt[t]{2}dt\Bigg]$$

Taking the antiderivative

$$\sum_{n=1}^\mathfrak{R} \sqrt[n]{2}=\lim_{N\to\infty}\Bigg[\sum_{n=1}^N \sqrt[n]{2}-\Bigg(\ln2\Big(\text{li}\ 2-\text{Ei}\frac{\ln2}{N}\Big)+N\sqrt[N]{2}-2\Bigg)\Bigg]$$

Moving some constants outside the limit

$$\sum_{n=1}^\mathfrak{R} \sqrt[n]{2}=2-\ln2\cdot\text{li}\ 2+\lim_{N\to\infty}\Bigg[\sum_{n=1}^N \sqrt[n]{2}-\Bigg(N\sqrt[N]{2}-\ln2\cdot\text{Ei}\frac{\ln2}{N}\Bigg)\Bigg]$$

It's at this point I'm unsure of how to proceed. I'm not terribly confident what the limit converges to. From my computational estimates up to $N=10^8$, I find that

$$\sum_{n=1}^\mathfrak{R} \sqrt[n]{2}\approx1.6$$

But due to floating point errors or slow convergence, it deviates substantially enough for me to not be confident about any more digits.

I'd like to know if this converges at all, and if it does, is there a (reasonably) closed form / relation to other constants?

from Hot Weekly Questions - Mathematics Stack Exchange Graviton from Blogger https://ift.tt/35hD4Fq

#Blogger

[ratnakarsadasyula-blog]

National Science Day

How many of us know about Dr.Yellapragada Subbarao whose work on methotrexate saved millions of cancer patients?

How many of are aware that J.C.Bose had invented the radio much earlier, but as he did not patent it, Marconi got the credit?

Do we know that S.N.Bose founded the field of Quantum Statistics, but did not get a Nobel for it, while those who did research on it got the Nobel?

Why did it take a foreigner to write a biography on Srinivasa Ramanujan, one of the greatest mathematicians of the modern era?

We know about Einstein, Euler, Edison, Fermi, Tesla, but nothing of our own Indian scientists who achieved against all odds?

Our scientists had to fight against racism, discrimination,lack of proper equipment,indifference and neglect. Not to mention the way the West tried to sabotage our space and nuclear program in every possible way.

On #NationalScienceDay, it is time to honor our scientists, recognize them for what they have achieved. To show the world, India is not just about spirituality, but also scientific progress. Instead of just hitting the Like or RT, button, please read this, think about it and share.

Our scientists have been the unsung heroes, contributing silently for the nation, it is time to honor them.

#national science day

[inkandcelluloid]

The man who knew infinity, directed by Matt Brown (2015).

Score: mediocre.

     The man who knew infinity is a biopic about Srinivasa Ramanujan, an Indian mathematician who made major contributions to mathematical analysis, number theory, infinite series, and continued fractions. He was compared to Euler and Jacobi by his peers, became a Fellow of the Royal Society and died of disease at age thirty-two. Now you know who the man was, I’m going to tell you why this movie sucks so hard.

     The movie opens with G. H. Hardy (Jeremy Irons) affably telling us how he didn’t invent Ramanujan (Dev Patel) but discovered him. This is a play on a later line that theorems are not invented but discovered that backfires horribly because it makes it look like Ramanujan would have not amounted to anything if Hardy hadn’t believed in him. Three cheers for The Good White Man! In real life, Ramanujan was a respected researcher in mathematics back in India, and it was the magnitude of his genius that drew attention to him from Europe. In the movie, he lives in a parody of India where if you know how to work an abacus you’re a genius. The Indian characters speaking English to each other in thick Indian accents made me cringe. Only twenty-odd minutes of the movie are spent in India, the audiences can endure twenty minutes of subtitles.

     In the movie, Ramanujan gets on the first ship out of Madras as soon as The Good White Man is interested in his work. In real life, it took some time to get him to move to Europe, partly for religious reasons and partly because I guess it’s hard to leave your family and friends behind for years even if The Good White Man is offering you a scholarship. The second act of the movie consists basically of The Good White Man defending The Poor Brown Man from The Chauvinists because hey, The Poor Brown Man might be brown, but that doesn’t mean he can’t be a genius. I’m sure Ramanujan suffered the effects of racism while he was in England, but there’s no way an obscure professor gets to bring a guy from India with a scholarship if there isn’t general consensus that the guy is good at what he does.

     Hardy and Ramanujan had different ways of working, as seen in the film: Hardy focused very hard on proof and rigour, while Ramanujan worked in a more intuitive way. But in real life, Hardy and Ramanujan were peers, not mentor and apprentice. Ramanujan didn’t have to prove anything to anyone, he was actually invited to Cambridge and awarded a PhD for his original research. This whole subplot where Hardy forces Ramanujan to write proofs for his theorems makes Hardy look condescending and Ramanujan whimsical and stubborn. Those dynamics would have been good in a story about a master and an apprentice, not coming from a researcher to another guy who’s having him for breakfast every day. Hell, if the guy is so good, just get him another person who writes proof for what he’s making, that’s actually the easy part.

     The third act of the movie focuses on Ramanujan’s illness and death, and on The Good White Man doing everything in his power to get The Poor Brown Man’s work acknowledged. In real life, Ramanujan was elected a member of the Royal Society because he rocked that hard, not because Hardy went around pestering people about it. In fact, he wasn’t even the first Indian to receive the honour. Also, the whole subplot with his mother hiding Janaki’s letters so he would come back sooner is just disgusting.

     A movie that should have been about an Indian genius and his eventual visit to Europe was made instead about how good a white man is for not being prejudiced and admitting that a non-white can be pretty smart too. And fighting for him, because he can’t!

     Last but not least, the movie says virtually nothing about Ramanujan’s work, which would be the most interesting thing about the movie (like with Emily Dickinson’s biopic). I really wish someone would start making biopics that actually said something about the person’s work. In a format similar to The big short, with some info dumps here and there that made science and art more approachable to people. Now that would be enjoyable to watch.

#the man who knew infinity #matt brown #films #reviews #srinivasa ramanujan #dev patel #toby jones #devika bhise #jeremy irons #biopic #mathematics

[startupupdates]

Ramanujan - The Indian genius who changed the world of mathematics

New Post has been published on https://startupupdates.info/ramanujan-the-indian-genius-who-changed-the-world-of-mathematics/

Ramanujan - The Indian genius who changed the world of mathematics

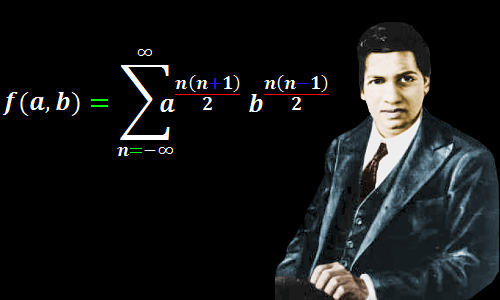
 In an interview by Paul Erdős, when Hardy was asked what his greatest contribution to mathematics was, Hardy unhesitatingly replied that it was the discovery of Ramanujan. So think how genius Ramanujan was , When one of greatest mathematician of 20th century unhesitatingly replied that his greatest contribution was not any mathematics discovery but discovery of one Indian genius.

Introduction

Srinivasa Ramanujan was born on December 22, 1887 and was predetermined to gotten to be a brilliant mathematician. Over the course of his life, he went on to create thousands of his own formulas, numerous of which have kept on be utilized in mathematics and science. In fact his Formula are indeed utilized to understand  dark holes. He initially made a few of his theories while in India , in spite of the fact that when he travelled to Cambridge in Britain to talk about his scientific equations with the brightest minds of the time, he made numerous there as well. It was in Britain that Ramanujan started  an inspirational partnership with the Cambridge teacher Godfrey Harold Hardy. Professor Hardy  figured it out that Ramanujan had found certain mathematical formulas by himself that were really as of now known to the mathematical elite. However, what was more striking was that he created his own formulas, which warranted further understanding. Most of his theories have been proven correct over time and have provided mathematicians since then with the basis from which to create formulas that continue to shape science today.

Early Life

Srinivasa Ramanujan was born in Erode, a city which is  presently in the Indian state of Tamil Nadu. His father, K. Srinivasa Iyengar, was a receptionist in a sari shop whereas his mother, Komalatammal, was a housewife who frequently sang religious hymns at the local Hindu temple. When he was just two years old, Ramanujan contracted smallpox and later recovered from the disease. As a child, he did not like attending school and his family even enlisted the help of a local constable to ensure that he actually attended. Paradoxically, it was at Kangayan Primary School that he really flourished. He performed very well academically. In November 1897, at nine years old, Ramanujan completed his primary school education and scored the highest marks in his local district. He then enrolled at Town Higher Secondary School. It was there that his love and fascination with mathematics began.

Ramanujan’s thirst for mathematical knowledge was unquenchable. By the age of 13, he had mastered a textbook by Professor Sidney Luxton Loney on advanced trigonometry, or the study of relationships involving the lengths and angles of triangles. Within a couple of years he was discovering complex mathematical theories on his own, creating his own formulas and even completed mathematical examinations in less than half the allocated time.

Ramanujan received a copy of A Synopsis of Elementary Results in Pure and Applied Mathematics by the mathematician George Shoobridge Carr from a friend. This contained a staggering 5,000 of Carr’s own theories. It is generally believed that by studying this book Ramanujan’s mathematical prowess was awakened. In 1904, he was awarded the K. Ranganatha Rao prize by his school’s headmaster, after which he received a scholarship at Government Arts College in Kumbakonam. While there he was so enamoured with mathematics that he neglected all other subjects, and subsequently lost his scholarship. Ramanujan would later enroll at Pachaiyappa’s College in Madras, now known as Chennai. He failed in his Fellow of Arts degree as he again did not perform well in subjects other than mathematics. He sat for the examinations again a year later but also failed. Since he lacked a degree, he left formal education to pursue his work independently and because he lacked formal qualifications, he concentrated on his theories alone, living in utter poverty and was often on the brink of starvation.

Adulthood

In 1909, at the age of 22, Ramanujan was married to Srimathi Janaki, also known as Janakiammal. At this time in history, it was not unusual for marriages to be arranged with girls who were much younger than the husband. This was the case for Ramanujan’s marriage to Srimathi Janaki who was only 10 years old at the time.

Following this, Ramanujan spent time looking for work in Chennai, while living in his friend’s house. At the same time, to earn some money, he gave tuition to students from Presidency College, one of the oldest government arts colleges in India and one of the two Presidency colleges established by the British. At that time the Indian Mathematical Society of India was formed by V. Ramaswamy Aiyer, whom Ramanujan met with when he was looking for a job. Later, Aiyer recalled looking through Ramanujan’s notebooks upon meeting him.

“I was struck by the extraordinary mathematical results contained in it [the notebooks]. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.”

This meeting was to be fortunate for Ramanujan, as he was soon sent to Chennai with letters of introduction from Aiyer. There he met with Aiyer’s mathematical peers, who again gave him letters of introduction and sent him to Raghunatha Ramachandra Rao, an Indian civil servant, mathematician and social and political activist and the secretary of the Indian Mathematical Society. Upon first meeting Ramanujan, Rao was unconvinced regarding his mathematical formulas and thought him a fraud. However upon talking and discussing various complicated mathematical theories with Ramanujan, he was won over by the young man’s mathematical genius. Ramanujan requested Rao’s help for financial aid while he continued his research and Rao happily obliged. This eventually led to Ramanujan having his work published in the Journal of the Indian Mathematical Society.

In 1912, Ramanujan applied for a temporary job in the Madras Accountant General’s office. There he was supposed to earn 20 Indian rupees a month, but he was only in this position for a couple of weeks. During this time, he applied for a job under the Chief Accountant of the Madras Port Trust. His application was accompanied by a letter of recommendation from Edgar William Middlemast, a professor of mathematics at Presidency College. This application landed Ramanujan a job as a Class III, Grade IV accounting clerk on March 1, 1912 with a monthly salary of 30 rupees. Ramanujan was adept at the work, finishing his assignments quickly, allowing him ample time to continue his research. His boss, Sir Francis Spring and his colleague, S. Narayana Iyer encouraged Ramanujan in his research.

In 1913, Diwan Bahadur Rao, Professor Middlemast and S. Narayana Iyer attempted to present Ramanujan’s work to various British mathematicians. Many of them ridiculed Ramanujan’s work, labelling him uneducated and a fraud. It was then that Ramanujan wrote to the mathematical elite at Cambridge University in England. Though he received the same negative reception from two professors, he received a warmer response from Professor Godfrey Harold Hardy. Though initially sceptical of Ramanujan’s work, upon analysing his manuscript further he was very impressed with some of his theories. Professor Hardy even stated that Ramanujan’s theories.

“defeated me completely; I had never seen anything in the least like them before”

and that his theories

“must be true, because, if they were not true, no one would have the imagination to invent them.”

After conferring with his colleague, Professor John Edensor Littlewood, who was equally impressed with Ramanujan’s work, Professor Hardy described him as a mathematician of the highest quality, a man whose work was original and powerful.

Professor Hardy wrote back to Ramanujan asking for more proof of his theories and began to arrange for Ramanujan to travel to Cambridge, contacting the Indian Office. Secretary Arthur Davies from the Advisory Committee for Indian Studies met with Ramanujan to discuss his trip to England, but Ramanujan refused to travel overseas to a foreign land, in observance of his strict Brahmin (priestly-caste) upbringing.

Despite this, Ramanujan felt very fortunate to have found such a friend. Professor Hardy even arranged, through his peers, for Ramanujan to receive a two-year research scholarship of 75 rupees a month from the University of Madras. While there he continued to submit papers containing his theories to the Journal of the Indian Mathematical Society.

There was a notable instance during which Ramanujan had pre-empted the work of another mathematician. Professor Edward Ross of Madras Christian College, who Ramanujan had met before, stormed into class one day. Flustered, he asked his students if Ramanujan knew Polish. It turned out that Ramanujan had written theories pre-empting the work of a Polish mathematician that had just arrived in the day’s mail.

Though dismayed at Ramanujan’s refusal to travel to Cambridge, Professor Hardy did not give up and enlisted the help of his colleague E. H. Neville. Over time, when Neville questioned Ramanujan regarding his refusal, it turned out that he no longer held reservations about traveling. Ramanujan promptly left for England, leaving his parents and wife behind in India.

Traveling to England and Life in Cambridge

Ramanujan’s journey from India to England took almost a whole month by sea. Traveling from Madras on March 17, 1914, he arrived in the ports of London on April 14. When he arrived, Ramanujan was whisked away to Cambridge after a couple of days stay in London. In Cambridge, Ramanujan was housed a short distance away from Professor Hardy’s own room. There he began working with Professor Hardy and Professor Littlewood almost immediately.

Studying his notebooks, they found many theories. Some had already been discovered by other mathematicians of the past, some they concluded were wrong and others they decided were complete breakthroughs. They were absolutely stunned by his brilliance, even comparing him to two of history’s most well-known mathematicians – Leonhard Euler and Carl Gustav Jacob Jacobi. Throughout Ramanujan’s time in England, Professor Hardy tried to provide Ramanujan with an education in the areas that he was not familiar with.

His five years spent in Cambridge was not without its difficulties. There was a clash of cultures between Ramanujan who came from a traditional Indian background and the two Cambridge professors. They had differences not only in the ways they worked together, but also in their beliefs. Ramanujan was a devout Hindu who relied on his intuition, whereas his colleague Professor Hardy was a stout atheist who only believed in what could be proven and in mathematics.

In March 1916, Ramanujan was awarded a PhD (then known as a Bachelor of Science) degree for his mathematical work, part of which was published as an academic paper in the journal Proceedings of the London Mathematical Society. This began a period of acceptance for Ramanujan and his work. He was elected to the London Mathematical Society in 1917, and then as Fellow of the Royal Society in 1918, the oldest scientific academy that still exists. He was only 31 years old at the time, making him one of the youngest Fellows since the Royal Society began in 1660. This award is only granted to those who have made a ‘substantial contribution to the improvement of natural knowledge, including mathematics, engineering science and medical science’. Other notable Fellows of the Royal Society include the likes of Sir Isaac Newton, Charles Darwin, Michael Faraday, Albert Einstein and Alan Turing. In 1918, Ramanuja made history by becoming the first ever Indian to be elected a Fellow of Trinity College, Cambridge.

Divine Mathematics

Ramanujan was born into a deeply religious Hindu family. Since his father spent most of the day at work, he was especially close to his mother. It was from her that he learned of the ancient Hindu tradition, learned to sing religious hymns, was encouraged to attend religious services at the local temples and learned the ways of the Brahmin (priestly) caste.

Ramanujan’s original refusal of Professor Hardy’s invitation to travel to England came about from his strict orthodox Hindu lifestyle, which prohibited him from travelling overseas. His parents also objected to this invitation, in accordance with their Brahmin upbringing.

However, his mother’s opposition was withdrawn after she received a dream from the family goddess, Namagiri, who told her not to stand in the way of her son and the fulfilment of his life’s purpose. Once he received her permission he promptly embarked on his journey that would bring him acclaim and establish his works among those of the world’s leading mathematical elite.

Following his deeply held beliefs, Ramanujan actually attributed his mathematical genius to this very same goddess, Namagiri. In fact he is known to have said,

“an equation for me has no meaning, unless it expresses a thought of God.”

Death and Acknowledgment

Ramanujan was never a very healthy person and suffered from illness and health issues throughout his life. This was exacerbated while in England, since he was not used to the foreign environment. He spent time at a sanatorium, or hospital for long-term illness after he was diagnosed with tuberculosis and a severe vitamin deficiency. Following this, he returned to India in 1919 but sadly, he passed away just a year later in 1920. He was 32 years old at the time of his passing. Ramanujan was survived by his wife Srimathi Janaki. Following an examination of his medical records, some experts have argued that his tuberculosis diagnosis was mistaken. They claim that he actually suffered from hepatic amoebiasis, a disease that could have been treated and even cured at the time.

Given his legacy as a great mathematician whose formulas still form the basis of many advanced equations and theories, his life and work have been celebrated in many ways. In 1962, the 75th anniversary of his birth, the Government of India released a memorial postal stamp in remembrance of his life and deeds. A new design of the stamp was released in 2011.

Learning institutions such as Government Arts College in Kumbakonam and IIT Madras in Chennai celebrate his achievements annually on what is referred to as Ramanujan Day. Various prizes for young mathematicians have also been started in his name, for example by the International Centre for Theoretical Physics, the SASTRA University and the Vasavi College of Engineering.

On December 22, 2011, the 125th anniversary of his birth, the Government of India declared that December 22 would be celebrated as ‘National Mathematics Day’ every year in honour of Srinivasa Ramanujan.