#math proofs

[knottybliss]

Good mornthing my darling thingmakers it is that day of days:

WIP WEDNESDAY

#wip wednesday #wednesday wip #sharing is caring #fiber arts #gardening #art #sculpture #math proofs #bread proofs #I want to see it alllllllll

[catscomputerscreativewriting]

It's so funny to me that people think of Math/Mathematicians as being hyper-logical and rational. Like, have you seen some of the wild things hiding in the Math?

Did you know there are non-computable numbers?? (https://en.wikipedia.org/wiki/Chaitin%27s_constant)

Did you know that there are things that are true, but we can't prove them??? (https://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems)

Did you know that we can prove that something exists, and yet never actually figure out what that thing is?? (https://mathworld.wolfram.com/NonconstructiveProof.html)

Math is crazy. Math is wild. Math hardly makes sense, and when you think you understand the weirdest parts of it, everyone who hears you explain it to thinks you're a gibbering lunatic.

"In mathematics you don’t understand things. You just get used to them." - von Neumann

(please share more unhinged math with me, i want to see more scary math)

#stem #math #mathblr #academics #mathematics #logic #stemblr #academia #proofs #computer science #theoretical computer science

[simplydnp]

who's hand is in this picture?

A Mathematically Rigorous Proof That I Spent Too Long Writing

welcome to university math: dnp hand edition

(no, don't leave, you'll be fine i promise)

to begin, we need a statement to prove. we have two options:

- the hand is dan's hand

- the hand is phil's hand

now, for most proofs in university math, you are told a true statement, and you must show why it is true using logic rules, definitions, and theorems. but, we do not know which of these statements are true, so we have to find out.

to prove that a statement is true, we must show that it is always true for the situation presented. to show a statement is false, we must present a single instance where the statement is false (also known as a counter example).

a quick not scary math example:

definition: a prime number is only divisible by 1 and itself.

statement: all prime numbers are odd

(this is false, because 2 is a prime number and it is even. you don't even need to check if there's any others, all you need is one single case where it isn't true to disprove it)

so now that we have a little background on proofs and how to prove and disprove them, we go back to our two statements.

the thing with this situation is, one of them must be true (unless you're gung-ho on someone else holding dan's face while phil takes a picture on his phone of dan in his glasses, in which case, i applaud your commitment, but in actuality this proof will cover that option too)

the full statement we have is: dan is touching his face or phil is touching dan's face

now, because this is Real Life and we have a picture where a hand is touching dan's face, we know already that one of these options is true (as mentioned above) but! using symbolic logic you could also come to this conclusion.

this type of statement is an 'or' statement, and if you're curious, you can look into 'truth-tables' and see why, but at least one of the options must be true.

back to the proof at hand (bah-duhm-tss)

okay. now, proofs also must be 'general' in order to mean anything, really. these are statements of truth of the universe, not just for individuals. so, we will prove this generally.

we have 2 people involved, so individual 1 (dan, the owner of the face and potential face toucher) will be labelled as 'D' , and individual 2 (phil, the possible face toucher who does not own the face) will be labelled as 'P'. thus, this can be true for any such D and any such P.

so with our 'or' statement, in order to prove it, we pick one of the options and say that it is not true, and we have to show then that the other is true.

step 1: let's assume this is not P's hand. (assumption)

step 2: thus, it must be D's hand. (what we take from our assumption)

step 3: now, if it is D's hand, we look at what a hand on one's own face is capable of appearing like. (a definition or true fact about step 2)

the position in the given photo shows the hand with a thumb on the cheek, and a finger on the forehead. so, we find an example of a person with their fingers in the same position (or close to) and see if this supports our claim.

consider:

now, with this image, you can clearly see how the subject's right hand has the thumb on the temple and index finger on the top of their head, however, it is a close enough position for our case.

from the view of the camera, the closest finger to the camera is the edge of the pinkie. in fact, it will always be the closest finger to the camera in this position, assuming the subject has all fingers and no additional appendages.

step 4: we now compare this to our photo (we verify if this holds to our claim or contradicts it)

in our photo, the closest appendage to the camera is the edge of the thumb.

step 5: thus, it cannot be the case that D is touching their own face. (what the evidence says)

step 6: as we assumed it was not P's hand and have shown it cannot be D's hand, and as this is an 'or' statement both of these claims cannot be false, we can therefore conclude it must be P's hand. (our conclusion: re-stating the statement and assumptions and conclusion)

step 7: we verify that P is true (optional step but in beginner proofs you generally show why your case works)

to do this, i will show a picture of a person touching another's face, and compare it to our image.

consider:

now, this image is not exactly the same, similar to above. however, P's left thumb is on the cheek, with their index on D's temple. the closest appendage to the camera (if it were in a similar perspective as our original) would be the edge of the thumb.

comparing it to our original:

our comparison holds.

thus, we can conclude that the true claim in this statement is that P must be touching D's face, which, in particular means that:

phil is touching dan's face in the image

thank you for partaking in phannie mathematics. we now know. i am not sorry.

bonus:

phil has a hitchhikers thumb and dan doesn't so why was this necessary at all 🤡

#genuinely might be my magnum opus #please don't be scared of the math there's not numbers if anything it's more logic than what most people would know as math #this was purely for fun. my brain just saw the anatomical options while ive been staring at that photo since we've gotten it #dan looks sooo good in phils glasses and i cant not think about it yknow #dan and phil if you read this. hi. hope you enjoyed the math lesson. loved the video btw. thank you for wdapteo 2023. #also shout out to all my other math major phannies. love you. hope you enjoyed #dnp #c.text #dan and phil #and for the hell of it: #math #mathematics #math proof

[max1461]

"Visual proofs", more commonly known as "examples",

#math #visual proof hateblog

[necromimetics]

I’m an enjoyer of applied math. Hypothetically. The problem is half the time I do applied math they’re like “so first we’re going to make 25 assumptions” and my pure math brain immediately violently recoils

#NO assumptions ONLY rigorous proof of EVERYTHING #what do you MEAN ‘close enough’ NO we must be rigorous about everything or I’ll DIE #math #pure math #sky.txt

[quintiple-a]

Guys math is just literal wizard shit. Like the way they can transmute numbers and invoke higher dimensions and conjure imaginary entities to elegantly solve a seemingly impossible problem…

It’s like “ha ha! I have constructed the impenetrable sphere! It is literally impossible to defeat it by brute force!” And then another guy is like :) and draws a funny shape and suddenly the whole sphere turns into a line and the wizard just goes around it and you’re like whaaaat. “Ah ha, but if I merely tesselate this periodic tiles like so…” and then it turns out a puzzle that has stumped scholars for ages is not only instantly resolved but opened up entire new worlds of research in the process.

This post brought to you by YouTube videos explaining math and physics concepts about things like the recently discovered aperiodic monotile

#math #science #physics #seriously one time a math video made me cry because the proof was so elegantly perfect and beautiful #and that was before I even started taking edibles #it felt as though I was peering into the very soul of the universe for a moment

[bubbloquacious]

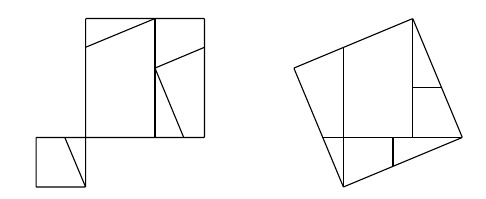
How do you guys like this very convoluted proof of the Pythagorean theorem I just made

#math #for my thesis btw hehe #one good thing about this one is that it is a direct scissors congruence using only translations #though there's definitely simpler diagrams that have that same property :p #this one i got by applying zylev's algorithm to the common visual proof where you add 4 triangles to make a square with side length (a+b)

[reesescuffs]

This

This is desert duo canon (I've only watched Scott third life you can trust me)

#this is my proof i can draw then normally #jay please believe me #mcyt #my draws #grian #gtwscar #ive never drawn desert duo before (pls trust i am truthful) #desert duo #my math book is um. almost soley grian draws u have a problem. 🥰😍

[felixcloud6288]

Did you know if a number is divisible by 3, you can add all the digits of the number and the sum is divisible by 3? For example, 327 is divisible by 3 and 3+2+7 = 12, which is divisible by 3.

For the Proof on why this is, click Read More

Prerequisite Knowledge

Numbers

Yes, I need to explain how numbers work for this proof.

Let's go back to elementary school. You're being taught basic addition of multi-digit numbers. You're given the number 54,321. 54,321 = 50,000 + 4,000 + 300 + 20 + 1

Let's expand that a little.

54,321 = 5*10,000 + 4*1,000 + 3*100 + 2*10 + 1

Now I''m going to take an aside and mention exponents, just in case.

Normal notation for exponents are a base number with a smaller number floating on the top right corner of your base value. Since Tumblr can't support that notation, I'll use a^b as the notation.

When you have an exponent, you have to multiply the base number by itself however many times the exponent number is. For example, 3^4 = 3*3*3*3 = 81.

Also, if the exponent value is 0 or smaller, you start dividing by the base number instead. So 3^0 = 3/3 = 1.

Now that I've explained that, let's go back to earlier.

54,321 = 5*10,000 + 4*1,000 + 3*100 + 2*10 + 1

Each digit in 54,321 is beling multiplied by an exponential power of 10.

54,321 = 5*10^4 + 4*10^3 + 3*10^2 + 2*10^1 + 1*10^0

This expanded form of an arbitrary number is going to be necessary for the proof.

Modulo and Equivalence

Let's go back to elementary school again. Remember how in division, you'd give a remainder as part of your answer? 12 / 5 = 2 remainder 2.

The modulo operator returns the remainder when you divide two numbers. In programming, % is used for modulo so I'll use that for notation. So 12 % 5 = 2.

An expansion of modulo is equivalence. Two numbers are equivalent under a modulo value when both numbers have the same remainder when divided by the modulo value. Under modulo value 5, 7 and 12 are equivalent because 7 % 5 = 2 and 12 % 5 = 2.

The normal notation for equivalence is the equal sign with 3 lines instead of 2. I'll use == for the notation here.

Since 7 and 12 are equivalent under mod 5, the notation is 7 == 12 (mod 5)

If a number is evenly divisible by a modulo power, it's equivalent to 0. 5 / 5 = 1, therefore 5 % 5 = 0, therefore 5 == 0 (mod 5)

There are some special rules about numbers that are equivalent. We'll let a, b, c, and m be arbitrary numbers.

If a == b (mod m), then a+c == b+c (mod m) If a == b (mod m), then a*c == b*c (mod m) If a == b (mod m), then a^c == b^c (mod m)

The Proof

Now let's move onto the proof.

Let's say we have some arbitrary whole number X which is divisible by 3. That means there is some whole number c such that X = 3*c. So if X is 327, c would be 109 because 109*3 = 327.

Now let's rewrite X into the expanded form from the Numbers section. We'll let d(0) refer to the least significant digit (The one at the far right). d(1) will be the next least significant digit and so on until we reach d(n), the most significant digit.

X = d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0

Since X is divisible by 3, that means the long form of X is equal to 3c.

d(n)*10^n + d(n-1)*10^(n-1) + … + d(1)*10^1 + d(0)*10^0 = 3*c

Now let's start doing some modulo.

10 == 1 (mod 3)

By the earlier rules mentioned in the Modulo section, we can multiply and exponentiate each term (The parts between the +) and they're still equivalent. So now we'll replace each term with an equivalent term under mod 3.

d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0 == d(n)*1^n + d(n-1)*1^(n-1) + … + d(1)*1^1 + d(0)*1^0 (mod 3)

1 exponentiated to any power is 1 so

d(n)*10^n + d(n-1)*10^(n-1) + ... + d(1)*10^1 + d(0)*10^0 == d(n) + d(n-1) + … + d(1) + d(0) (mod 3)

Meanwhile 3*c == 0 (mod 3). Since 3*c = X, then anything equivalent to X is equivalent to 0.

d(n) + d(n-1) + … + d(1) + d(0) == 0 (mod 3)

At this point we can say the sum of all the digits of X can be divided by 3 because the sum would have no remainder.

So in conclusion, if the sum of all the digits of a number can be divided by 3, then the number can be divided by 3.

#original post #mathematics #math proof #division

[lipshits-continuous]

Coming up with solutions to maths problems over text whilst half sleepy is a vibe honestly

#came up with the sketch of a near proof for why isolated subsets of R are countable #it's for my analysis homework and I'll do the fiddly details in the morning but the basic structure of the argument is there #maths posting #mathblr #maths #mathematics #lipshits posts

[noosphe-re]

In 1931, the Austrian logician Kurt Gödel pulled off arguably one of the most stunning intellectual achievements in history. Mathematicians of the era sought a solid foundation for mathematics: a set of basic mathematical facts, or axioms, that was both consistent — never leading to contradictions — and complete, serving as the building blocks of all mathematical truths. But Gödel’s shocking incompleteness theorems, published when he was just 25, crushed that dream. He proved that any set of axioms you could posit as a possible foundation for math will inevitably be incomplete; there will always be true facts about numbers that cannot be proved by those axioms. He also showed that no candidate set of axioms can ever prove its own consistency. His incompleteness theorems meant there can be no mathematical theory of everything, no unification of what’s provable and what’s true. What mathematicians can prove depends on their starting assumptions, not on any fundamental ground truth from which all answers spring.

Natalie Wolchover, How Gödel’s Proof Works, Quanta Magazine, July 14, 2020

#quote #mathematics #science #Kurt Godel #Kurt Gödel #Godel #Gödel #proof #truth #incompleteness theorem #theorem #Gödel's Incompleteness Theorems #Godel's Incompleteness Theorems #math #mathematician #logic #knowledge #ignorance #theory of everything

[humormehorny]

Why don’t they teach mathematical logic earlier? It’s present in literally all the books you have to read anyway. Some algebra author is going to be like for vs real numbers a,b ≠ 0 there exists a ratio a/b that is also a real number. And most people can’t even read that. Like half of the book is completely inaccessible because logic is fucking wild and requires actual practice with.

I’m not saying that this stuff is incredibly hard; it’s not. However logic just isn’t taught even though it is clearly foundational.

Sets especially seem to trigger me. Like I think a lot of people struggle with trig specifically because this aspect of functions is just not taught well. Like of course the arcsin(x) isn’t defined for -pi/2 > x < pi/2. It would be so much better if we actually taught this stuff.

#pretty frustrated #vent #mathematical logic #math #logic #mathblr #foundational mathematics #the more I read Hammock’s proof textbook #the angrier I get #this should have been taught at the bringing #there is nothing here that requires even algebra

[confusedcanaries]

Numbers! most of them are just sort of there

0 - 10/10 number, very useful, helps proving uniqueness, nicely splits the number line, breaks division which is very fun, additive identity

1 - 7/10 number, kinda the default, multiplicative identity, the induction engine

2 - 9/10 number, for all your actually a number needs, root-s nicely, 2+2=2*2=2^2 (chef's kiss), the only even prime, binary is hella funky (just to be clear though, this whole post is written in base-(# months from January to October inclusive))

3 - 6/10 number, sorta ok I guess, triangles are cool but this isn't a triangle just a triangle number, the other useful root, prime

4 to 10 - 5/10 numbers, sort of on a par with 3 but I might need to start using a calculator and beginning to get same-y.

Notable exceptions: 6=1+2+3=1*2*3 and 7 is just cool

>10 - 3/10 numbers, nothing really stands out here, I will get some slight anxiety if you ask me to do adding or multiplication with these without a calculator, just use induction at this point, this is not the sort of maths I chose maths to do.

The numbers you need complicated power series to reach or are defined ito functions - 10/10 numbers, fantastically unhelpful, really cool because these might as well be infinity and my brain can't cope (For Example: graham's number, googol, Tree(3), 52!)

-1 - 0/10 number (more like hellspawn), to say this is a number and not an inherently evil sentient object is false, hides itself in a minus sign, its entire purpose is to cause sign errors and make real analysis harder

Fractions - 7/10 numbers, rational is the new sexy, much better than decimals, somehow still a countable set despite being thicc in the reals (I know the term is dense but it's 1:30 in the morning, cut me some slack)

Irrationals - 5*sqrt(2)/10 numbers, slightly cooler and more mysterious than fractions, knows the uncomputable and normal numbers but won't tell you their addresses as you're just not cool enough

Mathematical constants - 6/10 numbers, useful but kinda like 3 in that they're a little boring. Some Exciting Constants: φ, Euler's Constant (γ), lemniscate constant (ϖ). Fun fact: e has a really cool continued fraction representation

Infinity - 11/10 concepts, maybe numbers - maybe not, so cool they deserve an illogical rating, gotta love the ordinals, countability is soooooooooo freaking cool (check out cantor's diagonalisation proof), I'm counting infinitesimal numbers as well here, also, the convention for just calling infinity one number for the complex numbers is hecking amazing

i - 7/10 number - very cool, philosophically taxing, the incredible original to the quaternions' disappointing sequel (maybe I'll change my mind when i actually learn about quaternions), geometry and rotation are now part of numbers! , makes differentiation so much more awesome

#math #mathblr #maths #numbers #what if this was what was originally meant by number theory #0 and infinity are the best #negative numbers although useful are incredibly annoying #I have found a truly marvellous proof this tag is too small to contain that all the opinions found above are objectively the truth

[oatbugs]

Jack Marsh (2005), Friendship Otherwise - Toward a Levinasian Description of Personal Friendship

#saw carnation lily lily rose by john singer seargent irl today. it was basically at my doorstep all along idk why i never went to see it #it was placed at a corner in the gallery. me and my friend sat down and sketched the paintings of beautiful naked people quite badly. paper #provided by tate britain. she told me about how she couldnt look her boyfriend in the face after a harrowing film about war. when i say the #interview was informal i mean the person who was supposed to be my boss told me let me get you a cider and then he said after #50 years of life he knows people are inherently good and it only takes a little bit of kindness to save this world. he said he tricked #his wife into keeping the baby and then he said he quit his job at a US bank to help people find meaning and in it #he would have liked to find meaning. instead he started climbing with his friends. he said he chews his cigarettes because its a habit from #when he had to hide things from people. the entire time i felt uncomfortable and incredibly enlightened. this is my friends mentor. she has #his pattern of pauses and expletive and penchant for ends-justify-means attitude. i do think im not very clever #but maybe one day i will love you enough to make up for it. i wrote code i dont understand staring at the final error i thought about how #we both thought of how when we're too old to remember the voices of our friends we would like to stand in the pathway of the LHC beam pipe #cut it open and eat light in the freezing cold vacuum (kills you long before radiation will) the invisible puncture wound unfolding dna #back to the start larger than you ever were. you go to heaven once youve been to hell. my friend is in my bed #practicing calculations of eigenvectors by hand and she is uninterested in a visual proof you are uninterested in incompetence #we catch a train this is your kind of burden you tragic hero wincing at that word you only do this because you have to. im the only one #who can. i am a coward in this for the fucking poetry. the visual proofs. the pretty numbers. an architect who was horrible at maths wanted #to be a philosopher and accidentally ended up neck in deep in 70th Error On Visual Studio Code i want to kiss your eyes before we say #goodbye we both know there is no love in the way there should be. I still have your dress in my wardrobe. i hope you make art. #you think im alright head-wise i think you fucking hate me i think ill never be so clever you want me to tell you my idea? #if you wanted more of this world i would have liked to kiss you harder. we cant both be like this. im sorry i cant be with you the whole wa #the love is gone if you have to ask it. his breath catches his eyes feel stiff it is -1.9 kelvin he is near the beam pipe i miss holding #his hand i miss her singing voice i miss his hair and i found the antonym of pain thank you for carrying me home.

[hand-face-chan]

I'm only halfway though Hbomberguy's new video and I dont know if this is a universal experience but my main horrified takeaway from hbomb's plagiarism video so far is that one of my highschools TAUGHT AN ENTIRE CLASS OF 13 YEAR OLDS TO PLAGIARISE. LIKE, ON PURPOSE.

I ended up moving to a much better highschool, but my first highschool essentially taught us to "write" essays by reading what someone else had written and then write what they said again but putting it "into your own words". Which in practice was teaching us to change, for example, "the works of Shakespeare were regarded by many as the first popular art form" to "Shakespeare's plays have been said by some to be the first example of popular media". One teacher actually told us that the process of writing an essay was "saying what the people you've researched have said, in a way where it sounds like you said it".

Like. The tactics that actual plagiarists use to hide the fact that they were stealing. An actual teacher tried to teach me to do that.

#hbomberguy #im so glad i left that school early the next year. it definitely would have gotten worse. #i literally didnt learn what a bibliography was until grade 9 because of how shit my first highschool was. #at the same time if a student wrote a paper that was 'too good' even if it was orginal theyd accuse them of stealing without proof #like i wrote a completely original paper and got the note 'this is very good - did you write it all yourself?' #fuck you man. yes i did. despite you trying to teach me to do the opposite #they accused me of getting my parents to write it for me. i had to show them everything i researched and my dad lost it at them #this was also the same school where they took every kid with a disability out of maths regardless of if they were good at maths or not #and taught them shapes like they were fucking three years old #i remember hanging out in the maths with all the other autistic kids and prentending to have never seen a triangle before for a joke #and while thats really bad and abelist. the non-disabled kids were still being taught addition and division like they were 8 and not 12 #the whole thing was a massive fuck up shit fest. it took the year 7 maths teacher leaving for us to all get the same maths class #and we STILL werent being taught to an age appropriate level because we missed so much grade 7 maths it had to be caught up in grade 8 #i would burn it down but its not a highschool anymore lol

[3-aem]

theres a thread on twitter rn explaining gojos technique that busts out how u arrive at eulers number and im just here like ur seriously gonna make me learn something via simping

this just proves if they wrote my college math textbooks in terms of fanfic i wouldnt have been barely passing freshman and sophomore year.

#i suck st math a lot #a bitch cant add cant write proofs can’t understand these hieroglyphs #long story short i was like oh thats what this number means #glad i gave yall my life savings to learn nothing