#physics

[mathani]

A rock is dropped from a tower one Earth's radius high and observed in the frame of the tower. Perhaps surprisingly the rock doesn't fall at the base of the tower. Ignoring resistance in the atmosphere it lands about 550 km to the East. This is because points closer to the axis move slower and the rock overtakes them. This is Coriolis force, which is not a force of interaction like gravity is. It's a consequence of observing a motion in the rotating frame of the Earth.

#gif #physics

[mindblowingscience]

By modifying a refrigerator commonly used in both research and industry, researchers at the National Institute of Standards and Technology (NIST) have drastically reduced the time and energy required to cool materials to within a few degrees above absolute zero. The scientists say that their prototype device, which they are now working to commercialize with an industrial partner, could annually save an estimated 27 million watts of power, $30 million in global electricity consumption, and enough cooling water to fill 5,000 Olympic swimming pools.

Continue Reading.

#Science #Physics #Quantum Physics #Technology #Energy #Refrigeration

[fuckyeahfluiddynamics]

Why Inkjet Paper Curls

Printed pages from inkjet printers tends to curl up over time. Researchers found that this long-term curl correlates with the migration of glycerol -- one of the solvents used in inkjet ink -- through the paper's fiber layers toward the unprinted side.  (Image credit: Lunghammer - TU Graz; research credit: A. Maass and U. Hirn; via Physics World) Read the full article

#fluid dynamics #glycerol #inkjet #paper #physics #porous flow #science #solid mechanics

[noosphe-re]

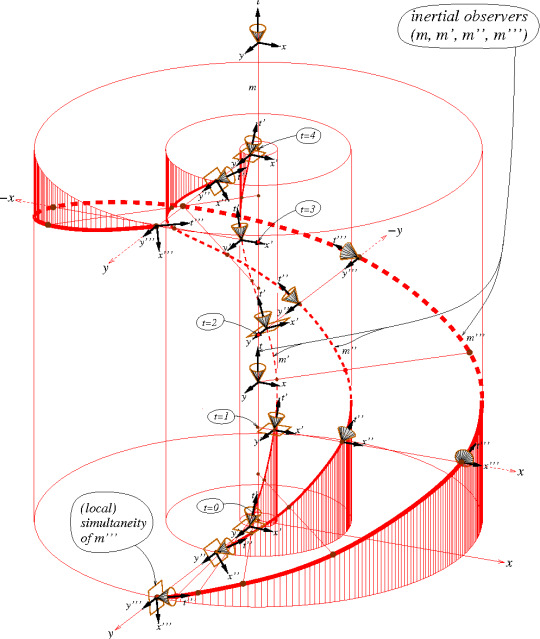
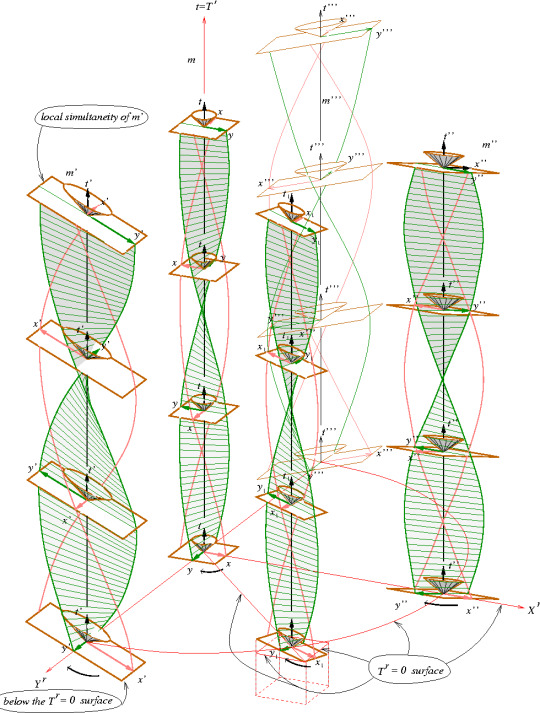
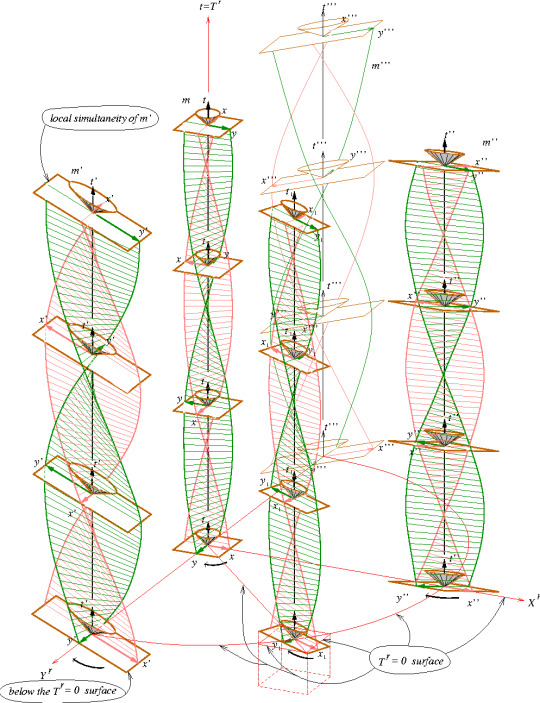
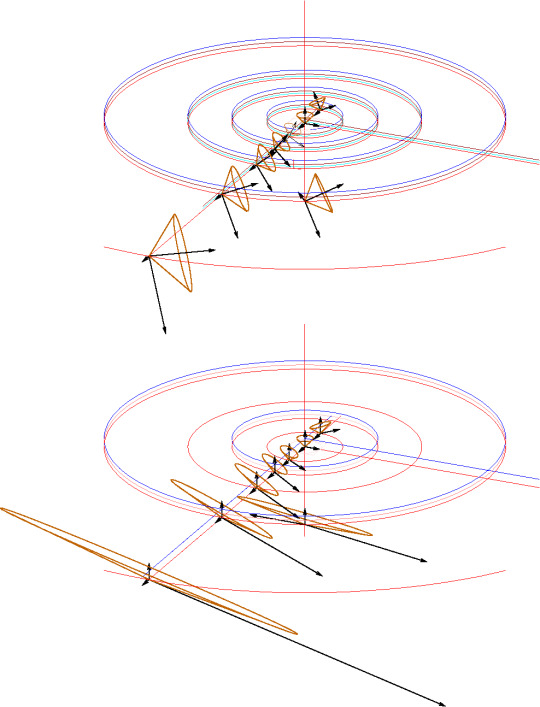
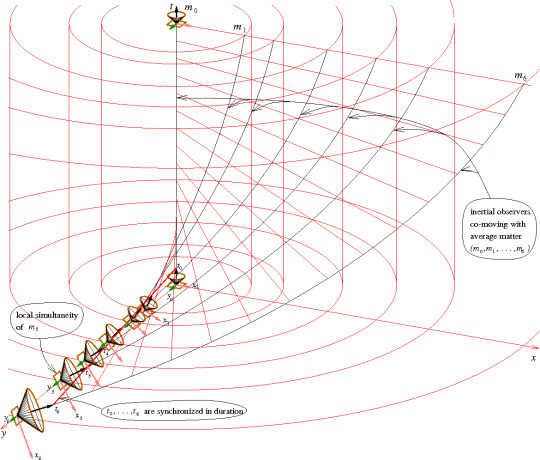
Németi, István et al. “Visualizing ideas about Gödel-type rotating universes.” (2009)

#science #physics #space time #universe #Godel #Kurt Godel #general relativity #Kurt Gödel #Gödel

[main-stop]

#acowar #french fries #twilight #KEITH #tyrus #西野七瀬 #spun alone #Ralph Lauren #joshua #choices #physics #motylki any

[resource-between-lawyer]

#emily sears #joji #matchablossom #instax #skam france #twilight #final fantasy vii #physics #the 100 #bucky barnes x reader #vanessa bohorquez #holland #13 reasons why

[studyblr-perhaps]

26/04/24 || Friday

I've not done 4 pictures in one post in a while haha. The 3rd picture is right after a storm so horrendous it tore off our hostel's false ceiling. Nature can be so horrifyingly beautiful.

The exam week is upon us, and I am trying to stay afloat. After this it's only one year before I graduate, and man I really want it to be over...

#studyblr #studyspo #studying #studyinspo #misa's undergrad journey #aesthetic #academia #physics #uni #study aesthetic #misa tries #stemblr #stem #women in stem

[political-past]

#acowar #sans au #spun alone #physics #sky ferreira #+18 or +adult only #girls who do dope #vanessa bohorquez #Jesus #humor #alexander the great #tom sturridge #briefs bulge

[hit-anything-wish]

#choices #physics #motylki any #bacon #sky ferreira #baekhyun #yennefer of vengerberg #kili #cullen rutherford #川崎あや

[interesting-science-might]

https://denise-298.ludgu.top/ln/SYMFqAl

#final fantasy vii #spun alone #tight butt #choices #physics #motylki any #bacon #the 100 #buddie #cullen rutherford #川崎あや #corgis #girls who do dope #parenting

[folgzstudies]

Prepared presentation for today’s experiment collaboration wok meeting.

Fortunately everything went smoothly 🤗

#physics studyblr #physics #student #study #notes #physics student #studyblr #study notes #thesis #flowers

[mathani]

You should start higher.

#gif #physics #no friction

[mindblowingscience]

The potential of quantum computing is immense, but the distances over which entangled particles can reliably carry information remains a massive hurdle. The tiniest of disturbances can make a scrambled mess of their relationship. To circumvent the problem, quantum computing researchers have found ways to stabilize long lengths of optical fibers or used satellites to preserve signals through the near-vacuum of space.

Continue Reading.

#Science #Technology #Physics #Quantum Physics #Quantum Computing

[fuckyeahfluiddynamics]

Geyser Sculptures

In the remote landscape of Tajikistan, photographer Øystein Sture Aspelund discovered a small geyser near a high-altitude lake. With a fast shutter, he "froze" the shapes of the eruption, capturing bubbly columns, mushrooms, and splashes. (Image credit: Ø. Aspelund; via Colossal) Read the full article

#bubble #fluid dynamics #fluids as art #geophysics #geyser #physics #science

[noosphe-re]

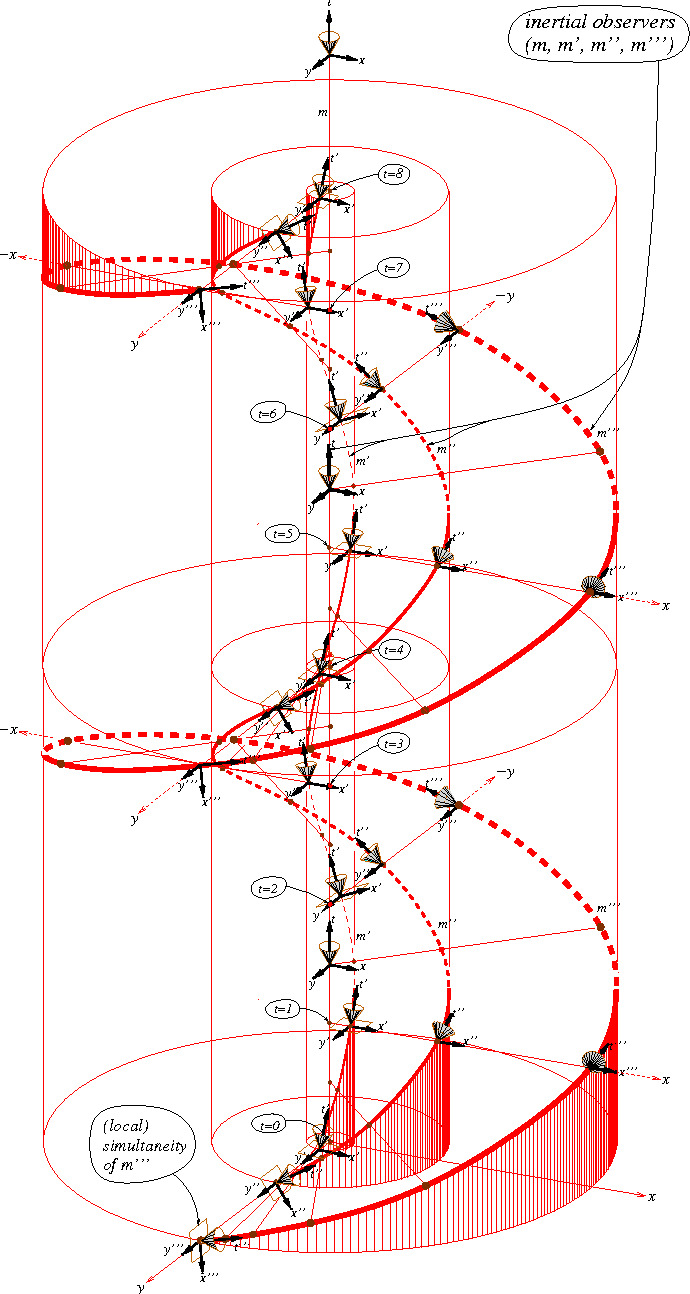
Figure 5: Previous figure copied on top of itself. It goes on like this in both directions forever. m′,m′′,m′′′ are (time-like worldlines of) observers “equivalent with” the observer m living on t̄. (Németi, István et al. “Visualizing ideas about Gödel-type rotating universes.” (2009))

#science #Kurt Godel #Godel #Kurt Gödel #physics #universe #space time #general relativity

[neosmanlymancave]

they’re everywhere (i am absolutely loosing my goddamn mind)

#wolfstar #sirius black #remus lupin #remus x sirius #marauders #astronomy #astrophysics #hl physics #physics #ib #international baccalaureate #ib diploma #ib dp #ib exams 2024 #ib year 2 #ibdp student