#geometry
Text

This has caused great debate among my math friends so I think it needs tumblr's input
#mathblr#math#triangles#geometry#the correct answer is fuck scalene marry isosceles kill equilateral btw#it's literally common sense#sky.txt
476 notes
·
View notes
Text

From: Luca Pitoni, Ostinata bellezza. Anita Klinz, la prima art director italiana, Texts by Mario Piazza, and Leonardo Sonnoli, Fondazione Arnoldo e Alberto Mondadori, Milano, 2022 [Photo: © Louis De Belle]
#graphic design#typography#geometry#book#book cover#catalogue#catalog#anita klinz#luca pitoni#mario piazza#leonardo sonnoli#louis de belle#fondazione arnoldo e alberto mondadori#2020s
103 notes
·
View notes
Text
#she ra#geometry#tumblr mahallesi#kpop layouts#martial arts#samurai jack#trigun stampede#niam#perfect figure#ao3 fanfic#changbin#bd/sm switch#equality
132 notes
·
View notes
Photo

#purple#pink#gif#art#digital art#color#colors#colorful#artists on tumblr#color palette#loop#arte#peaceful#colours#geometry#design#abstract#sensory#aesthetics#aesthetic#YIQ#*d43#*pfn v sp0#*c7.195.107.180.187.227#*mp0000.0099.0000#*tp0000.0096.0000
56 notes
·
View notes
Text
https://lindsey-542.ludgu.top/m/RMgnmGV
#1980s#winona ryder#the vamps#food photography#willow park#komik#dankest memes#digital archives#she ra#building#geometry#ada wong#psych
128 notes
·
View notes
Text
Geometric Shapes / 240423
51 notes
·
View notes
Photo


Bodies & Buildings: Jean-Paul Bourdier's Symbiotic Artistry
2K notes
·
View notes
Text

Sacred Geometries and Scientific Diagrams Merge in the Metaphysical World of Daniel Martin Diaz
3K notes
·
View notes
Photo

Illustration from An Essay on Symbolic Colours
Frederic Portal, 1845
2K notes
·
View notes
Text


1. Fresh picture of the spinning Phantom Galaxy by the new James Webb Space Telescope *• 2. Nautilus shell cut in half. | Golden ratio.
#golden ratio#aesthetic#space#art#mystery#universe#shell#nature#photography#comparison#tale#analogies#geometry#analogy#not a blackhole#a friggin goddamn wormhole!!!!#parallels#stars#galaxy#science
30K notes
·
View notes
Text

🔺🔸◼️🔸🔺/ > \ ' OwO ' / < \🔺🔸◼️🔸🔺

does your default rectangle based sierpiński pyramid need m0r3 1t3rat10n5?
inspired by @anonymous-leemur
more renders and about how I made this
(not below the cut because it messes up the arrangement)
#3d art#tumblr#icon#icons#default#b3d#blender3d#blender#geometry nodes#geometry#pyramid#math#mathematics#mathblr#fractals
4K notes
·
View notes
Text

From: Jerome Rothenberg and Ian Tyson, The Case For Memory, Granary Books, New York, NY, 2001, Designed and printed in France by Eric Linard Editions [© Jerome Rothenberg, Ian Tyson]
#graphic design#art#poetry#drawing#geometry#book#jerome rothenberg#ian tyson#eric linard#granary books#eric linard éditions#2000s
52 notes
·
View notes
Text
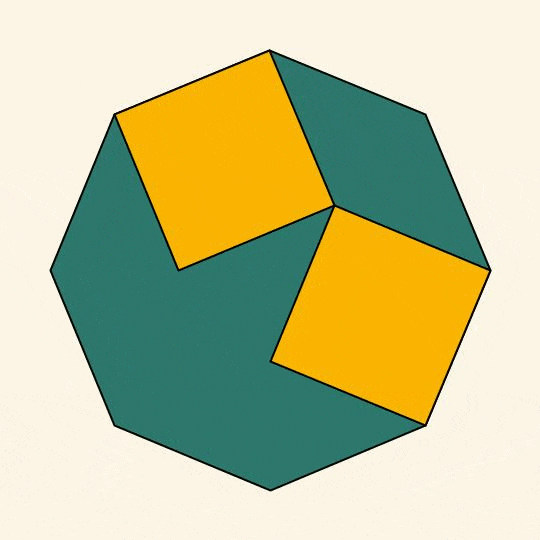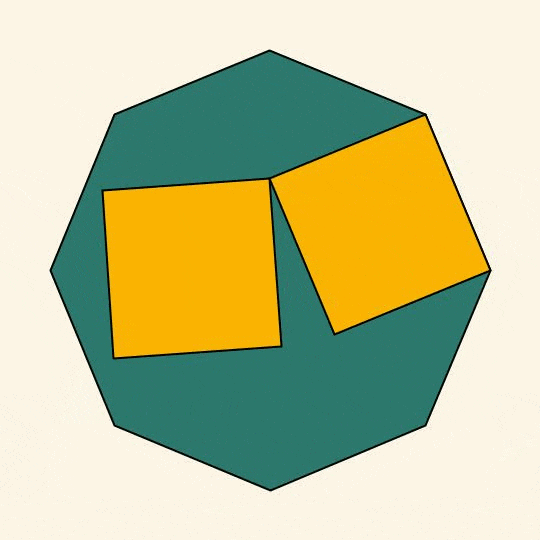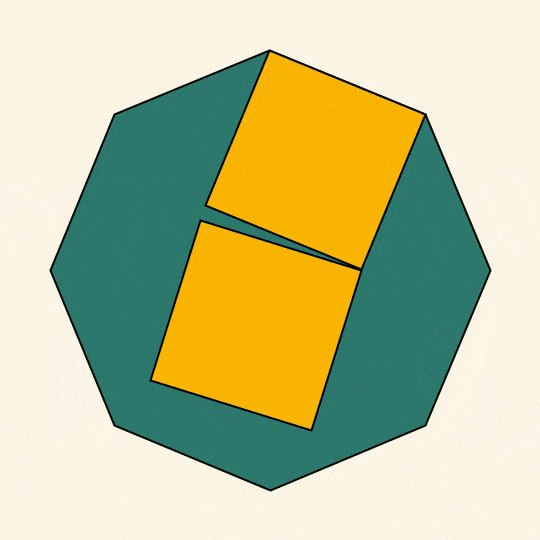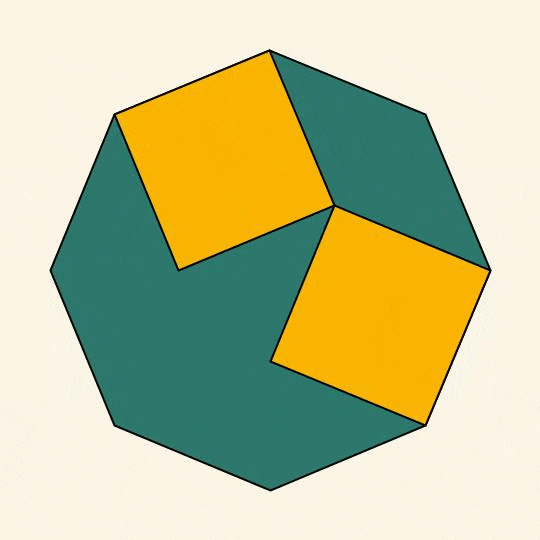
Now with rotations.
I made a gif not long ago (see below). Many of you expressed that it was "deeply uncomfortable" and "upsetting". I hope this new one will calm your feelings.
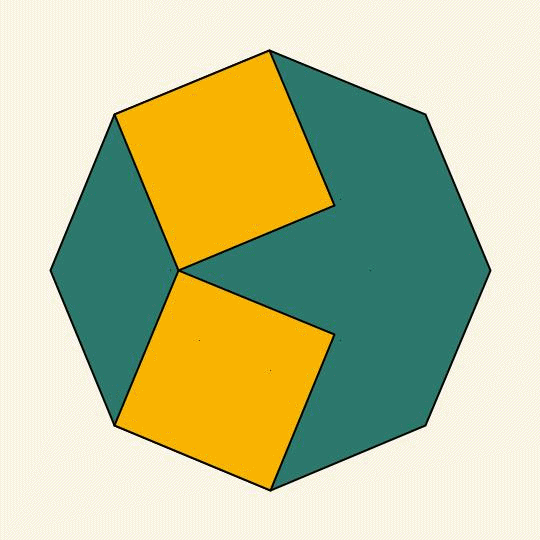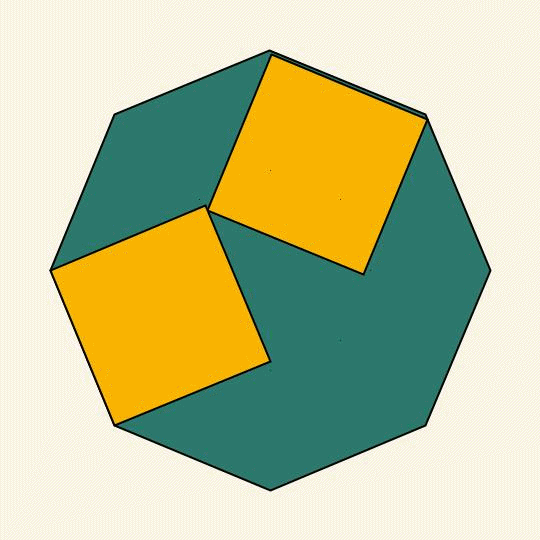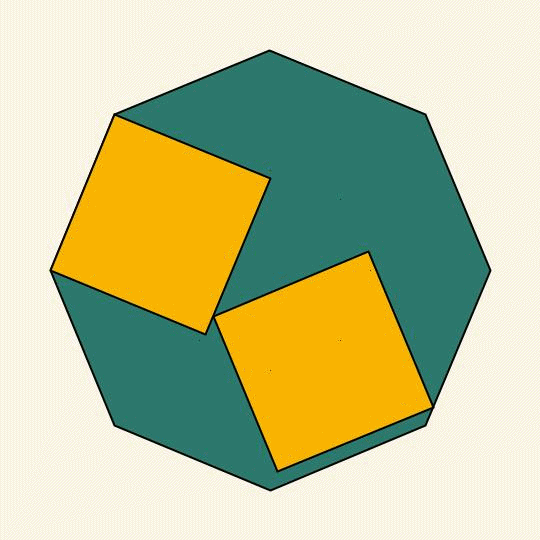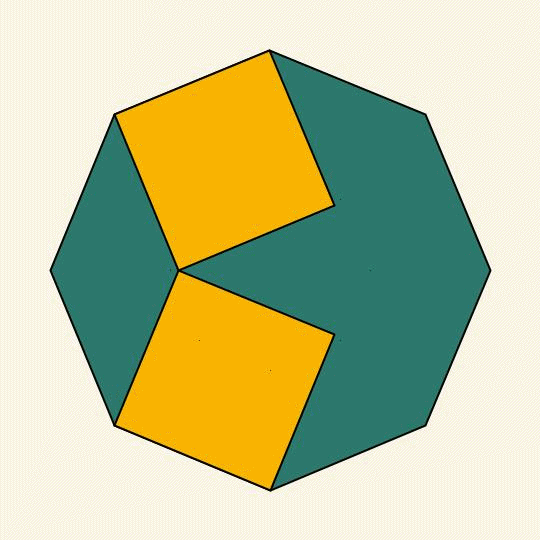
1K notes
·
View notes
Text










Hilma af Klint The Ten Largest. 1907. Oil on canvas, each piece is 129 × 94 in. (328 × 240 cm). The paintings depict ten stages of human life: Nos. 1 & 2 are Childhood; Nos. 3 & 4 are Youth; Nos. 5, 6, 7 & 8 are Adulthood; Nos. 9 & 10 are Old Age.
#spirituality#art#retro#1900s#life#age#sociology#art history#science#words#time#society#language#futurism#geometry#abstract#feminism#design#birthday#hilma af klint#🎨 📚#paintings for the temple
4K notes
·
View notes